题目内容
方程为 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为
,则该椭圆的离心率为
- A.

- B.

- C.

- D.

D
分析:先以圆为中心建立直角坐标系,则D,A,及两个焦点坐标可知,表示出 进而求得a和c关系,则离心率可得.
进而求得a和c关系,则离心率可得.
解答:以椭圆为中心建立直角坐标系,D(0,b),A(-a,0) F1(-c,0) F2(c,0)
∵
∴-3c=-a+2c
左右两边同除a推出 求得e= =
=
故选D
点评:圆锥曲线的概念与性质(特别是离心率)是高考的焦点,每年必考题.椭圆、双曲线、抛物线三种曲线都可能考查.
分析:先以圆为中心建立直角坐标系,则D,A,及两个焦点坐标可知,表示出
 进而求得a和c关系,则离心率可得.
进而求得a和c关系,则离心率可得.解答:以椭圆为中心建立直角坐标系,D(0,b),A(-a,0) F1(-c,0) F2(c,0)
∵

∴-3c=-a+2c
左右两边同除a推出 求得e=
 =
=
故选D
点评:圆锥曲线的概念与性质(特别是离心率)是高考的焦点,每年必考题.椭圆、双曲线、抛物线三种曲线都可能考查.

练习册系列答案
相关题目
 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )



 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )



 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )



 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )


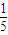
 的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若
的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )


