题目内容
下面四个判断:(1)(a4)
化简结果为
;(2)log(x+1)(x+1)=1成立的条件是x≠-1;(3)(
)2与log2
的大小关系是(
)2>log2
;(4)log2
+log23的值为-
.
其中正确的判断是
| 1 |
| 8 |
| a |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 24 |
| 5 |
| 2 |
其中正确的判断是
(3)、(4)
(3)、(4)
.分析:根据指数幂、对数的运算法则、指数函数、对数函数性质逐一判断,确定正确答案.
解答:解:(1)当a≥0时,(a4)
=a4×
=a
=
,当a≤0时,结果应为-
(2)log(x+1)(x+1)=1成立的条件是 x+1>0,且x+1≠1,即x>-1且x≠0
(3)由指数函数的性质,(
)2>0,由对数函数的性质,log2
<log21 =0,所以(
)2>log2
(4)log2
+log23=log2(
×3)=log2
=log2
-log28=
-3= -
.
故答案为:(3)、(4)
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| a |
| a |
(2)log(x+1)(x+1)=1成立的条件是 x+1>0,且x+1≠1,即x>-1且x≠0
(3)由指数函数的性质,(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(4)log2
| ||
| 24 |
| ||
| 24 |
| ||
| 8 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:(3)、(4)
点评:本题考查指数幂、对数的运算法则,指数函数、对数函数性质.要准确掌握应用有关法则和性质.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 化简结果为
化简结果为 ;(2)log(x+1)(x+1)=1成立的条件是x≠-1;(3)
;(2)log(x+1)(x+1)=1成立的条件是x≠-1;(3) 与
与 的大小关系是
的大小关系是 ;(4)
;(4)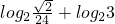 的值为
的值为 .
. 化简结果为
化简结果为 ;(2)log(x+1)(x+1)=1成立的条件是x≠-1;(3)
;(2)log(x+1)(x+1)=1成立的条件是x≠-1;(3) 与
与 的大小关系是
的大小关系是 ;(4)
;(4) 的值为
的值为 .
.