题目内容
设抛物线y2=4px(p>0)的准线与x轴的交点为M,过点M作直线l交抛物线于A,B两点.若直线l的斜率依次取p,p2,…,pn时,线段AB的垂直平分线与对称轴的交点依次为N1,N2,…,Nn,当0<p<1时,求S=
+
+…+
+…的值.
| 1 |
| |N1N2| |
| 1 |
| |N2N3| |
| 1 |
| NnNn+1 |
分析:根据题意,设直线l的方程为y=pn(x+p),与抛物线方程联解算出AB的中点坐标为(p(
-1),
),从而得到AB中垂直方程,然后在此方程中令y=0,得到得当斜率kn=pn时Nn的横坐标为(
+1)p.由此代入算出
关于p的表达式,证出{
}成公比为p2<1的等比数列,利用无穷递缩等比数列的求和公式即可算出S的值.
| 2 |
| p2n |
| 2p |
| pn |
| 2 |
| p2n |
| 1 |
| |NnNn+1| |
| 1 |
| NnNn+1 |
解答:解:∵抛物线y2=4px(p>0)准线为x=-p
∴M(-p,0),可得直线l的方程为y=pn(x+p)
与抛物线y2=4px消去x,得y2-
y+4p2=0
设A(x1,y1),B(x2,y2)
可得y1+y2=
,y1y2=4p2,所以x1+x2=
(y12+y22)=p(
-2)
∴线段AB的中点坐标为(
,
),即(p(
-1),
)
因此,线段AB的垂直平分线为y-
=
[x-p(
-1)]
令y=0,得xn=(
+1)p,得当斜率kn=pn时,Nn((
+1)p,0).
因此,|NnNn+1|=|xn+1-xn|=|(
+1)p-(
+1)p|=
(0<p<1),
所以
=
=
•(p2)n-1,
所以{
}是以
为首项,以p2为公比的等比数列,且0<p2<1,
故S=
+
+…+
+…=
=
.
∴M(-p,0),可得直线l的方程为y=pn(x+p)
与抛物线y2=4px消去x,得y2-
| 4p |
| pn |
设A(x1,y1),B(x2,y2)
可得y1+y2=
| 4p |
| pn |
| 1 |
| 4p |
| 4 |
| p2n |
∴线段AB的中点坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 2 |
| p2n |
| 2p |
| pn |
因此,线段AB的垂直平分线为y-
| 2p |
| pn |
| -1 |
| pn |
| 2 |
| p2n |
令y=0,得xn=(
| 2 |
| p2n |
| 2 |
| p2n |
因此,|NnNn+1|=|xn+1-xn|=|(
| 2 |
| p2n+2 |
| 2 |
| p2n |
| 2(1-p2) |
| p2n+1 |
所以
| 1 |
| |NnNn+1| |
| p2n+1 |
| 2(1-p2) |
| p3 |
| 2(1-p2) |
所以{
| 1 |
| NnNn+1 |
| p3 |
| 2(1-p2) |
故S=
| 1 |
| |N1N2| |
| 1 |
| |N2N3| |
| 1 |
| NnNn+1 |
| ||
| 1-p2 |
| p3 |
| 2(1-p2)2 |
点评:本题着重考查了抛物线的标准方程与简单几何性质、直线与圆锥曲线的位置关系、直线的斜率与等比数列的通项与求和公式等知识,属于中档题.本题综合了几何与代数中的主干知识,是一道不错的综合题型.

练习册系列答案
相关题目
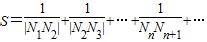 的值.
的值.