题目内容
已知函数f（x），对任意的实数x满足f（x-2）=f（x+2），且当x∈[-1，3）时，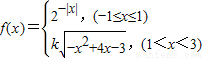
，若直线
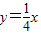与函数f（x）的图象有3个公共点，则实数k的取值范围为 ．
【答案】分析：确定函数的周期为4，分类讨论，作出函数的图象，k＞0时，问题转化为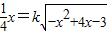
在（1，3）上有两个不等的实数根，
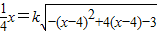在（5，7）上没有实数根，即可求得结论．
解答：解：∵对任意的实数x满足f（x-2）=f（x+2），∴f（x+4）=f（x），∴函数的周期为4
∵当x∈[-1，3）时，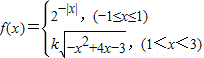
，
∴k＞0时，函数f（x）的图象如图所示
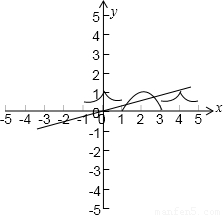
则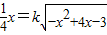
在（1，3）上有两个不等的实数根，
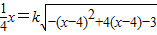在（5，7）上没有实数根
即（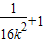
）x2-4x+3=0在（1，3）上有两个不等的实数根，（
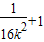）x2-12x+35=0在（5，7）上没有实数根
∴16-12（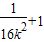
）＞0且144-140（
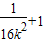）＜0
∵k＞0，∴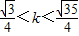
同理k＜0时，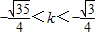
故答案为：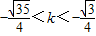
或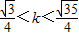
点评：本题考查函数图象的交点，考查数形结合的数学思想，考查学生的计算能力，属于中档题．
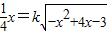在（1，3）上有两个不等的实数根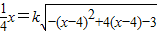，在（5，7）上没有实数根，即可求得结论．解答：解：∵对任意的实数x满足f（x-2）=f（x+2），∴f（x+4）=f（x），∴函数的周期为4
∵当x∈[-1，3）时，
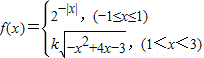，∴k＞0时，函数f（x）的图象如图所示
则
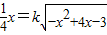在（1，3）上有两个不等的实数根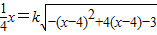，在（5，7）上没有实数根即（
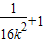）x2-4x+3=0在（1，3）上有两个不等的实数根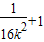，（）x2-12x+35=0在（5，7）上没有实数根∴16-12（
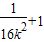）＞0且144-140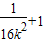（）＜0∵k＞0，∴
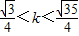
同理k＜0时，
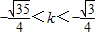
故答案为：
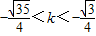或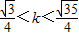点评：本题考查函数图象的交点，考查数形结合的数学思想，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目