题目内容
已知定义在R上的可导函数y=f(x)的导函数为f′(x),满足f′(x)<f(x),且y=f(x+1)为偶函数,f(2)=1,则不等式f(x)<ex的解集为( )A.(-∞,e4)
B.(e4,+∞)
C.(-∞,0)
D.(0,+∞)
【答案】分析:首先构造函数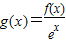 ,研究g(x)的单调性,结合原函数的性质和函数值,即可求解
,研究g(x)的单调性,结合原函数的性质和函数值,即可求解
解答:解:∵y=f(x+1)为偶函数
∴y=f(x+1)的图象关于x=0对称
∴y=f(x)的图象关于x=1对称
∴f(2)=f(0)
又∵f(2)=1
∴f(0)=1
设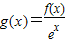 (x∈R),
(x∈R),
则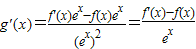
又∵f′(x)<f(x)
∴f′(x)-f(x)<0
∴g′(x)<0
∴y=g(x)单调递减
∵f(x)<ex
∴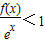
即g(x)<1
又∵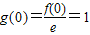
∴g(x)<g(0)
∴x>0
故答案为:(0,+∞)
点评:本题首先须结合已知条件构造函数,然后考察用导数判断函数的单调性,再由函数的单调性和函数值的大小关系,判断自变量的大小关系,属较难题
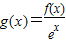 ,研究g(x)的单调性,结合原函数的性质和函数值,即可求解
,研究g(x)的单调性,结合原函数的性质和函数值,即可求解解答:解:∵y=f(x+1)为偶函数
∴y=f(x+1)的图象关于x=0对称
∴y=f(x)的图象关于x=1对称
∴f(2)=f(0)
又∵f(2)=1
∴f(0)=1
设
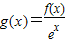 (x∈R),
(x∈R),则
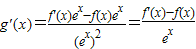
又∵f′(x)<f(x)
∴f′(x)-f(x)<0
∴g′(x)<0
∴y=g(x)单调递减
∵f(x)<ex
∴
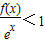
即g(x)<1
又∵
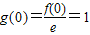
∴g(x)<g(0)
∴x>0
故答案为:(0,+∞)
点评:本题首先须结合已知条件构造函数,然后考察用导数判断函数的单调性,再由函数的单调性和函数值的大小关系,判断自变量的大小关系,属较难题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目