题目内容
设函数f(x)=xsinx(x∈R)则f(log 16),f(
16),f( ),f(
),f( )的大小关系为________(用“<”连接)
)的大小关系为________(用“<”连接)
f( )<f(log
)<f(log 16)
16)
分析:利用f′(x)=sinx+xcosx,利用f′( )<0,可分析出f(x)在(π,
)<0,可分析出f(x)在(π, ]上单调递减,从而使问题解决.
]上单调递减,从而使问题解决.
解答:∵f(-x)=-xsin(-x)=xsinx=f(x),
∴f(x)=xsinx为偶函数.
又log 16=
16=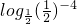 =-4,
=-4,
∴f(log 16)=f(-4)=f(4);
16)=f(-4)=f(4);
∵f′(x)=sinx+xcosx,
∴当∈(π, )时,sinx<0,cosx<0,
)时,sinx<0,cosx<0,
∴f′(x)=sinx+xcosx<0,
∴f(x)在(π, ]上单调递减,
]上单调递减,
又f′( )=sin
)=sin +
+ cos
cos =-
=- -
- ×
× <0,
<0,
∴当 <x≤
<x≤ ,f′(x)<0,
,f′(x)<0,
综上所述,当π<x≤ 时,f′(x)<0,
时,f′(x)<0,
∴f(x)在(π, ]上单调递减.
]上单调递减.
∵π< <4<
<4< ,
,
∴f( )>f(4)>f(
)>f(4)>f( );
);
故答案为:f( )<f(log
)<f(log 16)<f(
16)<f( ).
).
点评:本题考查不等式比较大小,考查导数的应用,利用导数分析得到f(x)在(π, ]上单调递减是关键,也是难点,属于难题.
]上单调递减是关键,也是难点,属于难题.
 )<f(log
)<f(log 16)
16)
分析:利用f′(x)=sinx+xcosx,利用f′(
 )<0,可分析出f(x)在(π,
)<0,可分析出f(x)在(π, ]上单调递减,从而使问题解决.
]上单调递减,从而使问题解决.解答:∵f(-x)=-xsin(-x)=xsinx=f(x),
∴f(x)=xsinx为偶函数.
又log
 16=
16=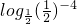 =-4,
=-4,∴f(log
 16)=f(-4)=f(4);
16)=f(-4)=f(4);∵f′(x)=sinx+xcosx,
∴当∈(π,
 )时,sinx<0,cosx<0,
)时,sinx<0,cosx<0,∴f′(x)=sinx+xcosx<0,
∴f(x)在(π,
 ]上单调递减,
]上单调递减,又f′(
 )=sin
)=sin +
+ cos
cos =-
=- -
- ×
× <0,
<0,∴当
 <x≤
<x≤ ,f′(x)<0,
,f′(x)<0,综上所述,当π<x≤
 时,f′(x)<0,
时,f′(x)<0,∴f(x)在(π,
 ]上单调递减.
]上单调递减.∵π<
 <4<
<4< ,
,∴f(
 )>f(4)>f(
)>f(4)>f( );
);故答案为:f(
 )<f(log
)<f(log 16)<f(
16)<f( ).
).点评:本题考查不等式比较大小,考查导数的应用,利用导数分析得到f(x)在(π,
 ]上单调递减是关键,也是难点,属于难题.
]上单调递减是关键,也是难点,属于难题. 
练习册系列答案
相关题目
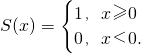 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).