题目内容
（2012•厦门模拟）已知函数f（x）=Asin（2x+θ），其中A≠0，θ∈(0，| π |
| 2 |
（I）若函数f（x）的图象过点E(-
| π |
| 12 |
| π |
| 6 |
| 3 |
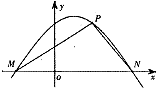
（Ⅱ）如图，点M，N分别是函数y=f（x）的图象在y轴两侧与x轴的两个相邻交点，函数图象上的一点P（t，
| ||
| 8 |
| PN |
| MN |
| ||
| 16 |
分析：（I）根据函数f（x）的图象过点E(-
，1)，F(
，
)，建立方程，可求θ的值，利用f(
)=
，可求A的值，从而可得函数解析式；
（Ⅱ）利用
•
=
，可求|NC|=
，从而|MC|=|MN|-|NC|=
，由此可得θ+2t=
，利用P（t，
）在图象上，即可求得函数f（x）的最大值．
| π |
| 12 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| 3 |
（Ⅱ）利用
| PN |
| MN |
| ||
| 16 |
| π |
| 8 |
| 3π |
| 8 |
| 3π |
| 4 |
| ||
| 8 |
解答：解：（I）∵函数f（x）的图象过点E(-
，1)，F(
，
)，
∴Asin（-
+θ）=1，Asin（
+θ）=
，
∴sin（
+θ）=
sin（-
+θ），
展开化简可得
cosθ=sinθ
∴tanθ=
∵θ∈(0，
)，∴θ=
∴函数f（x）=Asin（2x+
），
∵f(
)=
，∴A=2
∴f（x）=2sin（2x+
）；
（Ⅱ）设P在x轴上的射影为C，∵
•
=|
||
|cos∠PNM=
|NC|=
∴|NC|=
∴|MC|=|MN|-|NC|=
∴2[t-（-
）]-
=
∴θ+2t=
∵P（t，
）在图象上
∴Asin（θ+2t）=
∴A=
∴函数f（x）的最大值为
| π |
| 12 |
| π |
| 6 |
| 3 |
∴Asin（-
| π |
| 6 |
| π |
| 3 |
| 3 |
∴sin（
| π |
| 3 |
| 3 |
| π |
| 6 |
展开化简可得
| 3 |
∴tanθ=
| 3 |
∵θ∈(0，
| π |
| 2 |
| π |
| 3 |
∴函数f（x）=Asin（2x+
| π |
| 3 |
∵f(
| π |
| 6 |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
（Ⅱ）设P在x轴上的射影为C，∵
| PN |
| MN |
| PN |
| MN |
| π |
| 2 |
| π2 |
| 16 |
∴|NC|=
| π |
| 8 |
∴|MC|=|MN|-|NC|=
| 3π |
| 8 |
∴2[t-（-
| θ |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
∴θ+2t=
| 3π |
| 4 |
∵P（t，
| ||
| 8 |
∴Asin（θ+2t）=
| ||
| 8 |
∴A=
| ||
| 8 |
∴函数f（x）的最大值为
| ||
| 8 |
点评：本题考查三角函数的解析式，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目