题目内容
已知点M(a,b)在由不等式组
确定的平面区域内,则
的最大值为( )
|
| 4a+2b+16 |
| a+3 |
| A、4 | ||
B、
| ||
C、
| ||
D、
|
分析:画出可行域,将目标函数变形,赋予几何意义,是可行域中的点与点(-3,-2)连线的斜率的2倍加上4,由图求出取值范围.
解答:解:w=
=
=4+2×
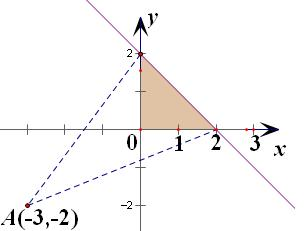
作出可行域,分析可得:
点(a,b)与点(-3,-2)确定的直线的
斜率为[
,
]
从而可以求得w的取值范围为[
,
]
则
的最大值为
故选D
| 4a+2b+16 |
| a+3 |
| 4(a+3)+2(b+2) |
| a+3 |
| b+2 |
| a+3 |

作出可行域,分析可得:
点(a,b)与点(-3,-2)确定的直线的
斜率为[
| 2 |
| 5 |
| 4 |
| 3 |
从而可以求得w的取值范围为[
| 24 |
| 5 |
| 20 |
| 3 |
则
| 4a+2b+16 |
| a+3 |
| 20 |
| 3 |
故选D
点评:本题考查画不等式组表示的平面区域,利用两点连线的斜率公式给目标函数赋予几何意义,数形结合求出范围.

练习册系列答案
相关题目