题目内容
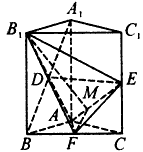
如图,已知在直三棱柱ABC- A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB= AA1,D、E、F分别为B1A、C1C、BC的中点。
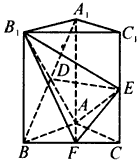
(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角B1-AE-F的余弦值。
(2)求证:B1F⊥平面AEF;
(3)求二面角B1-AE-F的余弦值。
| 解:(1)如图,连接A1E,并延长A1E交AC的延长线于点P,连接BP, 由E为C1C的中点,A1C1∥CP, 可得A1E=EP ∵D,E分别是A1B,A1P的中点, ∴DE∥BP, 又∵BP  平面ABC,DE 平面ABC,DE 平面ABC, 平面ABC,∴DE∥平面ABC。 |
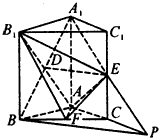 |
| (2)∵△ABC是等腰直角三角形,∠BAC=90° F为BC的中点, ∴BC⊥ AF, 又∵B1B⊥平面ABC, 由三垂线定理可得B1F⊥AF 设AB=AA1=2,则B1F=  ,EF= ,EF=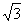 ,B1E=3, ,B1E=3, ∴B1F2+EF2=B1E2, ∴B1F⊥EF, ∵AF∩EF=F, ∴B1F⊥平面AEF; |
|
| (3)如图过F作FM⊥AE于点M,连接B1M ∵B1F⊥平面AEF,由三垂线定理可得 B1M⊥AE, ∴∠B1MF为二面角B1-AE-F的平面角 又C1C⊥平面ABC,AF⊥FC,由三垂线定理可得EF⊥AF, 在Rt△AEF中,可求得 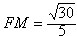 在Rt△B1FM中,∠B1FM=90° ∴ 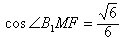 ∴二面角B1-AE-F的余弦值为 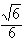 。 。 |
 |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB= 如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,
如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°, 如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为