题目内容
如图,已知直线a∥平面α;求证:过a有且只有一个平面平行于α.
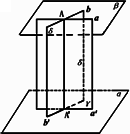
答案:
解析:
解析:
|
证明:(1)存在性:设过a的平面 (2)唯一性:设过a还有一个平面π∥α,∵π与δ有公共点A,∴π与δ相交于过A的直线 |

练习册系列答案
相关题目
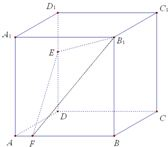 8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )
8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )

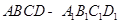 中,
中,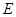 ,
,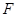 分别为 棱
分别为 棱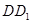 ,
,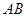 上的点. 已知下列判断:
上的点. 已知下列判断: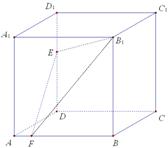
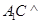 平面
平面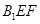 ;②
;②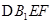 在侧面
在侧面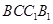 上 的正投影是面积为定值的三角形;③在平面
上 的正投影是面积为定值的三角形;③在平面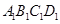 内总存在与平面
内总存在与平面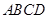 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点