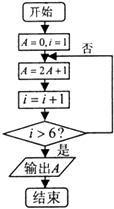
题目内容
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=![]() , AB=2,CD=3,M为PC上一点,PM=2MC.
, AB=2,CD=3,M为PC上一点,PM=2MC.
(Ⅰ)证明:BM∥平面PAD;
(Ⅱ)若AD=2,PD=3,求二面角D﹣MB﹣C的正弦值.
【答案】证明:(1)在DC上取点E,使DE=2,
则DE∥AB,DE=AB,
则四边形ABED是平行四边形,
则EB∥AD,
∵![]() ,∴PD∥ME,
,∴PD∥ME,
则平面PAD∥平面MBE,
∵BM平面MBE,BM平面PAD,
∴BM∥平面PAD
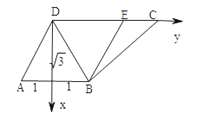
(2)△ABD是正三角形,建立以D为坐标原点的空间直角坐标系如图: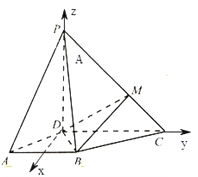
则B(![]() ,1,0),P(0,0,3),C(0,3,0),M(0,2,1),
,1,0),P(0,0,3),C(0,3,0),M(0,2,1),![]() =(
=(![]() ,1,0),
,1,0),![]() =(0,2,1),
=(0,2,1),
设平面DBM的法向量为![]() =(x,y,z),
=(x,y,z),
则由![]()
![]() =
=![]() x+y=0,
x+y=0,![]()
![]() =2y+z=0,得
=2y+z=0,得![]() ,
,
令x=1,则y=﹣![]() ,z=2
,z=2![]() 则
则![]() =(1,﹣
=(1,﹣![]() ,2
,2![]() ),
),
设平面MBC的法向量为![]() =(x,y,z),
=(x,y,z),![]() =(﹣
=(﹣![]() ,2,0),
,2,0),![]() =(0,1,﹣1),
=(0,1,﹣1),
则![]()
![]() =﹣
=﹣![]() x+2y=0,
x+2y=0,![]()
![]() =y﹣z=0,
=y﹣z=0,
令x=2,则y=![]() ,z=
,z=![]() ,
,
即![]() =(2,
=(2,![]() ,
,![]() ),
),
则cos<![]() ,
,![]() >=
>=![]() =
=![]() =
=![]() =
=![]() ,
,
则二面角D﹣MB﹣C的正弦值sinα=![]() =
=![]() .
.
即平面ACD与平面BCD所成的锐二面角的余弦值是![]() .
.
【解析】(Ⅰ)根据线面平行的判定定理即可证明BM∥平面PAD;
(Ⅱ)若AD=2,PD=3,建立空间直角坐标系求出平面的法向量,利用向量法即可求二面角D﹣MB﹣C的正弦值。

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式![]()
![]() 与用水量
与用水量![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )
)
附:参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: