题目内容
设命题![]() 关于
关于![]() 的二次方程
的二次方程![]() 的一个根大于零,另一根小于零;命题
的一个根大于零,另一根小于零;命题![]() 不等式
不等式![]() 对
对![]() 上恒成立,如果命题“
上恒成立,如果命题“![]() ”为真命题, 命题“
”为真命题, 命题“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
解:令![]() ,因为关于
,因为关于![]() 的二次方程
的二次方程![]() 的一个根大于零,另一根小于零,所以
的一个根大于零,另一根小于零,所以![]() ,即:
,即:![]() ,解得:命题
,解得:命题![]() 为真时
为真时![]()
………3分
因为![]() ,所以由不等式
,所以由不等式![]() 可得:
可得:![]() ,令
,令![]() ,由
,由![]() 在
在![]() 上单调递增,故
上单调递增,故![]() .又不等式
.又不等式![]() 对
对![]() 上恒成立,所以命题
上恒成立,所以命题![]() 为真时
为真时![]() . ………7分
. ………7分
因为命题“![]() ”为真命题, 命题“
”为真命题, 命题“![]() ”为假命题,所以
”为假命题,所以
(1)若![]() 真
真![]() 假,得
假,得![]()
(2)若![]() 假
假![]() 真,得
真,得![]() .
.
综上可得:![]() 或
或![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,设P:函数
,设P:函数 在R上单调递减,
在R上单调递减, 的一元二次方程
的一元二次方程 有两个不相等的实数根,
有两个不相等的实数根, ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. ,设P:函数
,设P:函数 在R上单调递减,
在R上单调递减, 的一元二次方程
的一元二次方程 有两个不相等的实数根,
有两个不相等的实数根, ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数c的取值范围.
”为假命题,求实数c的取值范围. ,设P:函数
,设P:函数 在R上单调递减,Q:关于
在R上单调递减,Q:关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,如果命题“
有两个不相等的实数根,如果命题“ ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. ,设P:函数
,设P:函数 在R上单调递减,Q:关于
在R上单调递减,Q:关于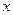 的一元二次方程
的一元二次方程 有两个不相等的实数根,如果命题“
有两个不相等的实数根,如果命题“ ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.