题目内容
在Rt△ABC中,AC=2,BC=2,已知点P是△ABC内一点,则
•(
+
)的最小值是( )
| PC |
| PA |
| PB |
分析:分别以CB,CA所在的直线为x,y轴建立直角坐标系,然后利用向量的数量积的坐标表示求解
•(
+
),根据两点间的距离公式即可求解
| PC |
| PA |
| PB |
解答: 解:分别以CB,CA所在的直线为x,y轴建立直角坐标系
解:分别以CB,CA所在的直线为x,y轴建立直角坐标系
∵AC=BC=2
∴A(0,2),C(0,0),B(2,0)
设P(x,y),则
=(-x,2-y),
=(2-x,-y)),
=(-x,-y)
∴
+
=(2-2x,2-2y)
∴
•(
+
)=-x(2-2x)-y(2-2y)
=-2x+2x2-2y+2y2
=2(x-
)2+2(y-
)2-1
即(x-
)2+(y-
)2为△ABC内一点到点(
,
)距离平方,当其最小时向量
•(
+
)最小,
因为点(
,
)也在△ABC内,
所以(x-
)2+(y-
)2最小为0,所以向量
•(
+
)的最小值为-1
故选B
 解:分别以CB,CA所在的直线为x,y轴建立直角坐标系
解:分别以CB,CA所在的直线为x,y轴建立直角坐标系∵AC=BC=2
∴A(0,2),C(0,0),B(2,0)
设P(x,y),则
| PA |
| PB |
| PC |
∴
| PA |
| PB |
∴
| PC |
| PA |
| PB |
=-2x+2x2-2y+2y2
=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
即(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PC |
| PA |
| PB |
因为点(
| 1 |
| 2 |
| 1 |
| 2 |
所以(x-
| 1 |
| 2 |
| 1 |
| 2 |
| PC |
| PA |
| PB |
故选B
点评:本题主要考查了向量的数量积的坐标表示的应用,解题的关键是根据所求式子 几何意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
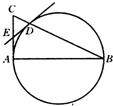 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.