题目内容
现有7名奥运会志愿者,其中志愿者A1,A2,A3通晓日语,B1,B2通晓俄语,C1,C2通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求A1被选中的概率;
(Ⅱ)求B1和C1不全被选中的概率.
解:(Ⅰ)从7人中选出通晓日语、俄语和韩语的志愿者各1名,其一切可能的结果组成的基本事件空间
Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),
(A2,B1,C1),(A2,B1,C2),(A,2,B2,C1),(A2,B2,C2),
(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2)},
由12个基本事件组成,它们的发生时等可能的.用M表示“A1被选中”,
则M={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2)}共4个位基本事件,
故P(M)= =
=
(Ⅱ)用N表示“B1和C1不全被选中”,则其对立事件 表示“B1和C1全被选中”,
表示“B1和C1全被选中”,
由于 ={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,
={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,
故P( )=
)=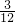 =
= ,由对立事件的概率公式可得P(N)=1-P(
,由对立事件的概率公式可得P(N)=1-P( )=1-
)=1- =
=
分析:(Ⅰ)列举出所有的基本事件,找出“A1被选中”的基本事件数,由概率公式可得;
(Ⅱ)用N表示“B1和C1不全被选中”,则其对立事件 表示“B1和C1全被选中”,先求P(
表示“B1和C1全被选中”,先求P( ),再由对立事件的概率公式可得答案.
),再由对立事件的概率公式可得答案.
点评:本题考查列举法求等可能事件的概率,利用对立事件的概率来求是解决问题的关键,属基础题.
Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),
(A2,B1,C1),(A2,B1,C2),(A,2,B2,C1),(A2,B2,C2),
(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2)},
由12个基本事件组成,它们的发生时等可能的.用M表示“A1被选中”,
则M={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2)}共4个位基本事件,
故P(M)=
 =
=
(Ⅱ)用N表示“B1和C1不全被选中”,则其对立事件
 表示“B1和C1全被选中”,
表示“B1和C1全被选中”,由于
 ={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,
={={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}共3个基本事件,故P(
 )=
)=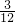 =
= ,由对立事件的概率公式可得P(N)=1-P(
,由对立事件的概率公式可得P(N)=1-P( )=1-
)=1- =
=
分析:(Ⅰ)列举出所有的基本事件,找出“A1被选中”的基本事件数,由概率公式可得;
(Ⅱ)用N表示“B1和C1不全被选中”,则其对立事件
 表示“B1和C1全被选中”,先求P(
表示“B1和C1全被选中”,先求P( ),再由对立事件的概率公式可得答案.
),再由对立事件的概率公式可得答案.点评:本题考查列举法求等可能事件的概率,利用对立事件的概率来求是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目