题目内容
过点P(-2,3)且与两坐标轴围成的三角形面积为12的直线共有____条.
- A.1
- B.2
- C.3
- D.4
C
分析:设直线的斜率为k,则有直线的方程为y-3=k(x+2),由直线过点P(-2,3)且与两坐标轴围成的三角形面积为12求出k的值有3个,从而得出结论.
解答:过点P(-2,3)且与两坐标轴围成的三角形面积为12的直线的斜率为k,则有直线的方程为y-3=k(x+2),
即 kx-y+2k+3=0,它与坐标轴的交点分别为M(0,2k+3)、N(-2-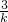 ,0).
,0).
再由 12= =
= |2k+3|×|-2-
|2k+3|×|-2-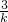 |,可得|4k+
|,可得|4k+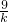 +12|=24,4k+
+12|=24,4k+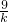 +12=24,或 4k+
+12=24,或 4k+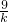 +12=-24.
+12=-24.
解得 k= ,或 k=
,或 k= 或 k=
或 k= ,
,
故满足条件的直线有3条,
故选C.
点评:本题主要考查用点斜式求直线方程的方法,体现了分类讨论的数学思想,属于基础题.
分析:设直线的斜率为k,则有直线的方程为y-3=k(x+2),由直线过点P(-2,3)且与两坐标轴围成的三角形面积为12求出k的值有3个,从而得出结论.
解答:过点P(-2,3)且与两坐标轴围成的三角形面积为12的直线的斜率为k,则有直线的方程为y-3=k(x+2),
即 kx-y+2k+3=0,它与坐标轴的交点分别为M(0,2k+3)、N(-2-
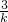 ,0).
,0).再由 12=
 =
= |2k+3|×|-2-
|2k+3|×|-2-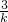 |,可得|4k+
|,可得|4k+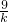 +12|=24,4k+
+12|=24,4k+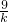 +12=24,或 4k+
+12=24,或 4k+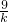 +12=-24.
+12=-24.解得 k=
 ,或 k=
,或 k= 或 k=
或 k= ,
,故满足条件的直线有3条,
故选C.
点评:本题主要考查用点斜式求直线方程的方法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目