题目内容
已知等差数列{an}的前n项和为Sn,且a4=9,S5=35
(1)求{an}的通项公式;
(2)记bn= ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn
(3)对任意正整数n,不等式 -
- ≤0成立,求正数a的取值范围.
≤0成立,求正数a的取值范围.
解:(1)由已知可得a1=3,d=2,∴an=2n+1
(2)由(1)得Sn=n2+2n,bn= ,∴
,∴ ;
;
(3)由已知得 ,
,
设 ,则
,则 ,
,
∴数列{cn}递增,∴cn的最小值为c1=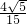 ,
,
∴只需
分析:(1)利用等差数列的通项及前n项和公式可求;
(2)先求得Sn=n2+2n,,从而可表示 ,利用裂项求和法易求;
,利用裂项求和法易求;
(3)先分离参数为 ,再构造函数,利用函数的最小值解决恒成立问题.
,再构造函数,利用函数的最小值解决恒成立问题.
点评:本小题主要考查数列的求和、函数单调性的应用、数列与不等式的综合等基础知识,考查运算求解能力,考查方程思想、化归与转化思想
(2)由(1)得Sn=n2+2n,bn=
 ,∴
,∴ ;
;(3)由已知得
 ,
,设
 ,则
,则 ,
,∴数列{cn}递增,∴cn的最小值为c1=
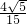 ,
,∴只需

分析:(1)利用等差数列的通项及前n项和公式可求;
(2)先求得Sn=n2+2n,,从而可表示
 ,利用裂项求和法易求;
,利用裂项求和法易求;(3)先分离参数为
 ,再构造函数,利用函数的最小值解决恒成立问题.
,再构造函数,利用函数的最小值解决恒成立问题.点评:本小题主要考查数列的求和、函数单调性的应用、数列与不等式的综合等基础知识,考查运算求解能力,考查方程思想、化归与转化思想

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.