题目内容
在△ABC中，a+b=10，cosC是方程2x2-3x-2=0的一个根，求①角C的度数，
②△ABC周长的最小值．
【答案】分析：①由cosC是方程2x2-3x-2=0的一个根可求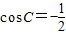
，在△ABC中可求C
②由余弦定理可得：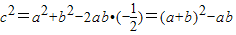
，由a=5时，及c最小且可求，进而可求△ABC周长的最小值
解答：解：①∵2x2-3x-2=0∴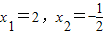
…（2分）
又∵cosC是方程2x2-3x-2=0的一个根∴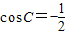
，
在△ABC中∴C=120度…（7分）
②由余弦定理可得：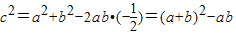
即：c2=100-a（10-a）=（a-5）2+75…（10分）
当a=5时，c最小且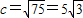
此时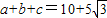
…（12分）
∴△ABC周长的最小值为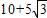
…（14分）
点评：本题主要考查了三角形中由三角函数值求解角，余弦定理的应用，属于公式的简单运用，属于基础试题
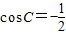，在△ABC中可求C②由余弦定理可得：
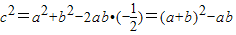，由a=5时，及c最小且可求，进而可求△ABC周长的最小值解答：解：①∵2x2-3x-2=0∴
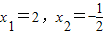…（2分）又∵cosC是方程2x2-3x-2=0的一个根∴
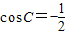，在△ABC中∴C=120度…（7分）
②由余弦定理可得：
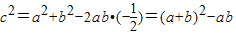
即：c2=100-a（10-a）=（a-5）2+75…（10分）
当a=5时，c最小且
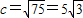此时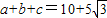…（12分）∴△ABC周长的最小值为
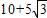…（14分）点评：本题主要考查了三角形中由三角函数值求解角，余弦定理的应用，属于公式的简单运用，属于基础试题
练习册系列答案
相关题目