题目内容
已知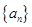 为等比数列,
为等比数列,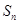 是它的前
是它的前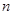 项和.若
项和.若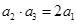 ,且
,且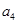 与
与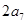 的等差中项为
的等差中项为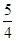 ,则
,则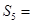
| A.35 | B.33 | C.31 | D.29 |
C
解析试题分析:用a1和q表示出a2和a3代入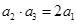 求得a4,再根据a4+2a7=a4+2a4q3,求得q,进而求得a1,代入S5即可解:a2•a3=a1q•a1q2=2a1,∴a4=2,a4+2a7=a4+2a4q3=2×
求得a4,再根据a4+2a7=a4+2a4q3,求得q,进而求得a1,代入S5即可解:a2•a3=a1q•a1q2=2a1,∴a4=2,a4+2a7=a4+2a4q3=2×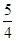
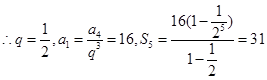 ,故可知答案为C.
,故可知答案为C.
考点:等比数列
点评:本题主要考查了等比数列的性质.属基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知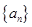 是各项均为正数的等比数列,
是各项均为正数的等比数列,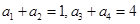 ,则
,则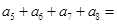
| A.20 | B.32 | C.80 | D.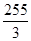 |
已知实数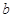 是
是 和
和 的等比中项,则
的等比中项,则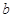 =
=
A. | B.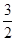 | C. | D.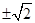 |
已知等比数列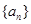 满足
满足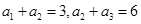 ,则
,则 ( )
( )
| A.64 | B.81 | C.128 | D.243 |
已知实数列-1,x,y,z,-2成等比数列,则xyz等于
| A.-4 | B.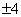 | C.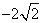 | D.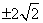 |
已知数列{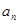 }满足
}满足 ,且
,且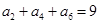 ,则
,则 的值是( )
的值是( )
A.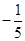 | B.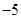 | C.5 | D.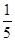 |
在各项都为正数的等比数列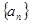 中,首项
中,首项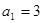 ,前三项和为21,则
,前三项和为21,则 =( )
=( )
| A.33 | B.72 | C.84 | D.189 |
已知等比数列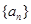 满足
满足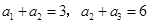 ,则
,则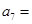 ( )
( )
| A.64 | B.81 | C.128 | D.243 |