题目内容
已知定义在 上的可导函数
上的可导函数 的导函数为
的导函数为 ,满足
,满足 ,且
,且 为偶函数,
为偶函数, ,则不等式
,则不等式 的解集为 .
的解集为 .
 .
.
解析试题分析:令 ,∴
,∴ ,∴
,∴ 在
在 上单调递减,又∵
上单调递减,又∵ 是偶函数,∴
是偶函数,∴ ,∴
,∴ ,
,
∴ ,即不等式
,即不等式 的解集为
的解集为 .
.
考点:利用导数判断函数单调性.

练习册系列答案
相关题目
已知函数 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 在(1,1)处的切线方程为( )
在(1,1)处的切线方程为( )
A. | B. |
C. | D. |
函数 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.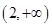 | D.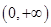 |
下列函数中周期为 且为偶函数的是( )
且为偶函数的是( )
A. | B. |
C. | D. |
若 中
中 ,点
,点 为
为 边中点,且
边中点,且 ,
, ,则
,则 的面积等于( ).
的面积等于( ).
| A.2 | B.3 | C. | D. |
 的
的 的取值集合是 .
的取值集合是 . 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的图像可能是( ) .
的图像可能是( ) .


