题目内容
已知a，b∈R+，函数f(x)=
(x∈R)．
（1）判断函数f（x）的单调性，并证明你的结论；
（2）比较
与
的大小．
| ax+1+bx+1 |
| ax+bx |
（1）判断函数f（x）的单调性，并证明你的结论；
（2）比较
| a2+b2 |
| a+b |
| ab |
（1）函数f(x)=
(x∈R)递增函数，证明如下：
设x＜y，则x-y＜0，f(x)-f(y)=
，
①当a=b时，f（x）为常数函数，此时不单调．
②若a＞b，则a-b＞0，ax-y＜bx-y，ax-y-bx-y＜0，所以f（x）＜f（y），
此时函数f(x)=
(x∈R)递增函数．
③当a＜b，则a-b＜0，ax-y＞bx-y，ax-y-bx-y＞0，所以f（x）＜f（y），
此时函数f(x)=
(x∈R)递增函数．
（2）
-
=
=
=
，
因为幂函数x
，x
在（0，+∞）上单调递增，具有相同的单调性．
所以当a=b时，
=
．
当a≠b时，
＞
．
| ax+1+bx+1 |
| ax+bx |
设x＜y，则x-y＜0，f(x)-f(y)=
| (a-b)(ax-y-bx-y)ayby |
| (ax+bx)(ay+by) |
①当a=b时，f（x）为常数函数，此时不单调．
②若a＞b，则a-b＞0，ax-y＜bx-y，ax-y-bx-y＜0，所以f（x）＜f（y），
此时函数f(x)=
| ax+1+bx+1 |
| ax+bx |
③当a＜b，则a-b＜0，ax-y＞bx-y，ax-y-bx-y＞0，所以f（x）＜f（y），
此时函数f(x)=
| ax+1+bx+1 |
| ax+bx |
（2）
| a2+b2 |
| a+b |
| ab |
a2+b2-a
| ||||
| a+b |
a2+b2-a
| ||||||||
| a+b |
(a
| ||||||||
| a+b |
因为幂函数x
| 3 |
| 2 |
| 1 |
| 2 |
所以当a=b时，
| a2+b2 |
| a+b |
| ab |
当a≠b时，
| a2+b2 |
| a+b |
| ab |
练习册系列答案
备战中考寒假系列答案
相关题目
=（x，1），
=（-1，b-x），函数f（x）=a-
是偶函数．
=（x，1），
=（-1，b-x），函数f（x）=a-
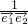是偶函数．