题目内容
函数f(x)对任意x∈R都有f(x)+f(1-x)= ,数列{an}满足:
,数列{an}满足: ,运用课本中推导等差数列前n项和公式的方法,可求得an=________.
,运用课本中推导等差数列前n项和公式的方法,可求得an=________.

分析:由于f(x)+f(1-x)=
 ,由于an=f(0)+f(
,由于an=f(0)+f( )+f(
)+f( )+…+f(
)+…+f( )+f(1),an=f(1)+f(
)+f(1),an=f(1)+f( )+…+f(
)+…+f( )+f(
)+f( )+f(0),利用倒序相加法即可求得an.
)+f(0),利用倒序相加法即可求得an.解答:∵函数f(x)对任意x∈R都有f(x)+f(1-x)=
 ,数列{an}满足:
,数列{an}满足: ①,
①,∴an=f(1)+f(
 )+…+f(
)+…+f( )+f(
)+f( )+f(0)②,
)+f(0)②,∴①+②得:
2an=[f(0)+f(1)]+[f(
 )+f(
)+f( )]+[f(
)]+[f( )+f(
)+f(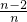 )]+…+[f(
)]+…+[f( )+f(
)+f( )]+[f(1)+f(0)]=(n+1)×
)]+[f(1)+f(0)]=(n+1)× ,
,∴an=
 .
.故答案为:
 .
.点评:本题考查数列求和,着重考查倒序相加法,熟练应用“f(x)+f(1-x)=
 ”是关键,属于中档题.
”是关键,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目