题目内容
设集合M=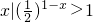 ; N={x|x2-2x-3≤0},则N∩(CRM)=
; N={x|x2-2x-3≤0},则N∩(CRM)=
- A.(1,+∞)
- B.(-∞,-1)
- C.[-1,1]
- D.(1,3)
C
分析:将集合M中不等式右边的数字利用零指数公式化简,利用以 为底数的指数函数为减函数转化为关于x的不等式,求出不等式的解集确定出集合M,由全集R,求出M的补集,求出集合N中不等式的解集,确定出集合N,找出M补集与N的公共部分,即可求出所求的集合.
为底数的指数函数为减函数转化为关于x的不等式,求出不等式的解集确定出集合M,由全集R,求出M的补集,求出集合N中不等式的解集,确定出集合N,找出M补集与N的公共部分,即可求出所求的集合.
解答:∵集合M中的函数( )1-x>1=(
)1-x>1=( )0,且以
)0,且以 为底数的指数函数为减函数,
为底数的指数函数为减函数,
∴1-x<0,即x>1,
∴集合M=(1,+∞),又全集为R,
∴CRM=(-∞,1],
由集合N中的不等式x2-2x-3≤0,变形得:(x-3)(x+1)≤0,
解得:-1≤x≤3,
∴集合N=[-1,3],
则N∩(CRM)=[-1,1].
故选C
点评:此题属于以指数函数的单调性及一元二次不等式的解法为平台,考查了交、并、补集的混合运算,是高考中常考的基本题型.
分析:将集合M中不等式右边的数字利用零指数公式化简,利用以
 为底数的指数函数为减函数转化为关于x的不等式,求出不等式的解集确定出集合M,由全集R,求出M的补集,求出集合N中不等式的解集,确定出集合N,找出M补集与N的公共部分,即可求出所求的集合.
为底数的指数函数为减函数转化为关于x的不等式,求出不等式的解集确定出集合M,由全集R,求出M的补集,求出集合N中不等式的解集,确定出集合N,找出M补集与N的公共部分,即可求出所求的集合.解答:∵集合M中的函数(
 )1-x>1=(
)1-x>1=( )0,且以
)0,且以 为底数的指数函数为减函数,
为底数的指数函数为减函数,∴1-x<0,即x>1,
∴集合M=(1,+∞),又全集为R,
∴CRM=(-∞,1],
由集合N中的不等式x2-2x-3≤0,变形得:(x-3)(x+1)≤0,
解得:-1≤x≤3,
∴集合N=[-1,3],
则N∩(CRM)=[-1,1].
故选C
点评:此题属于以指数函数的单调性及一元二次不等式的解法为平台,考查了交、并、补集的混合运算,是高考中常考的基本题型.

练习册系列答案
相关题目
 ,N =
,N = ,则 ( )
,则 ( )  N C.M
N C.M N D.M
N D.M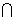 N=
N=
 ; N=
; N= ,
则
,
则
 B.
B. C.
C. D.
D.
 ,N =
,N = , 则--(
)
, 则--(
) N C. N
N C. N N=
N=