题目内容
已知向 ,
, 满足|
满足| |=1,|
|=1,| |=6,且
|=6,且 •(
•( -
- )=2,求:
)=2,求:
(1) 与
与 的夹角;
的夹角;
(2)|2 -
- |的模.
|的模.
解:(1)∵ •(
•( -
- )=
)= •
• -
- 2=2,
2=2,
又| |=1,|
|=1,| |=6
|=6
∴ •
• =3,即|
=3,即| ||
|| |cos<
|cos< ,
, >=3,解得cos<
>=3,解得cos< ,
, >=
>=
又0≤< ,
, >≤π,所以
>≤π,所以 与
与 的夹角为
的夹角为
(2)|2 -
- |2=4
|2=4 2-4
2-4 •
• +
+ 2=28,
2=28,
∴|2 -
- |=2
|=2
分析:(1)由题意,可根据题中条件求出 •
• ,再由数量积公式即可求出
,再由数量积公式即可求出 与
与 的夹角;
的夹角;
(2)先对|2 -
- |平方,再将两向量的内积与模代入计算求出模.
|平方,再将两向量的内积与模代入计算求出模.
点评:本题考查平面向量数量积的运算及其定义,解题的关键是根据题设条件解出两向量的内积及掌握平方法求向量的模
 •(
•( -
- )=
)= •
• -
- 2=2,
2=2,又|
 |=1,|
|=1,| |=6
|=6∴
 •
• =3,即|
=3,即| ||
|| |cos<
|cos< ,
, >=3,解得cos<
>=3,解得cos< ,
, >=
>=
又0≤<
 ,
, >≤π,所以
>≤π,所以 与
与 的夹角为
的夹角为
(2)|2
 -
- |2=4
|2=4 2-4
2-4 •
• +
+ 2=28,
2=28,∴|2
 -
- |=2
|=2
分析:(1)由题意,可根据题中条件求出
 •
• ,再由数量积公式即可求出
,再由数量积公式即可求出 与
与 的夹角;
的夹角;(2)先对|2
 -
- |平方,再将两向量的内积与模代入计算求出模.
|平方,再将两向量的内积与模代入计算求出模.点评:本题考查平面向量数量积的运算及其定义,解题的关键是根据题设条件解出两向量的内积及掌握平方法求向量的模

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 ,
, 满足|
满足| |=1,|
|=1,| |=6,且
|=6,且 (
( ﹣
﹣ )=2,求:
)=2,求: 与
与 的夹角;
的夹角; ﹣
﹣ |的模.
|的模.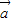 ,
,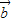 满足:
满足: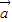 +
+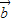 =(1,3),
=(1,3),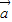 -
-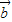 =(3,-3),则
=(3,-3),则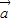 、
、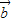 的坐标分别为( )
的坐标分别为( )