题目内容
已知函数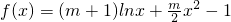 .
.
(1)当 时,求f(x)在区间
时,求f(x)在区间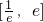 上的最值;
上的最值;
(2)讨论函数f(x)的单调性.
解:(1)当 时,
时,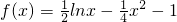
∴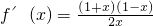
∵x>0,∴x+1>0
∴令f′(x)>0,即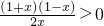 ,∵x>0,x+1>0,∴0<x<1;
,∵x>0,x+1>0,∴0<x<1;
令f′(x)<0,即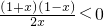 ,∵x>0,x+1>0,∴x>1,
,∵x>0,x+1>0,∴x>1,
∴函数的递增区间为(0,1),递减区间为(1,+∞)
∵x∈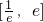
∴函数的递增区间为[ ,1),递减区间为(1,e]
,1),递减区间为(1,e]
∴f(x)在区间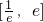 上的最大值为f(1)=-
上的最大值为f(1)=- ,最小值为f(e)=
,最小值为f(e)=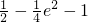 ;
;
(2)∵函数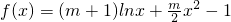 ,
,
∴ (x>0)
(x>0)
当m≥0时,f′(x)>0,函数在(0,+∞)上单调递增;
当-1<m<0时, ,
,
令f′(x)>0,∵x>0,-1<m<0,∴0<x< ;
;
令f′(x)<0,∵x>0,-1<m<0,∴x> ;
;
∴函数在(0, )上单调递增,在(
)上单调递增,在( ,+∞)上单调减;
,+∞)上单调减;
当m≤-1时,f′(x)≤0,函数在(0,+∞)上单调递减.
分析:(1)求导函数,确定函数在区间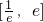 上的单调性,即可求最值;
上的单调性,即可求最值;
(2)求导函数,对m分类讨论,利用导数的正负,可得函数f(x)的单调性.
点评:本题考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.
 时,
时,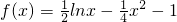
∴
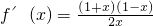
∵x>0,∴x+1>0
∴令f′(x)>0,即
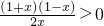 ,∵x>0,x+1>0,∴0<x<1;
,∵x>0,x+1>0,∴0<x<1;令f′(x)<0,即
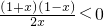 ,∵x>0,x+1>0,∴x>1,
,∵x>0,x+1>0,∴x>1,∴函数的递增区间为(0,1),递减区间为(1,+∞)
∵x∈
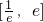
∴函数的递增区间为[
 ,1),递减区间为(1,e]
,1),递减区间为(1,e]∴f(x)在区间
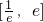 上的最大值为f(1)=-
上的最大值为f(1)=- ,最小值为f(e)=
,最小值为f(e)=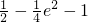 ;
;(2)∵函数
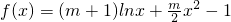 ,
,∴
 (x>0)
(x>0)当m≥0时,f′(x)>0,函数在(0,+∞)上单调递增;
当-1<m<0时,
 ,
,令f′(x)>0,∵x>0,-1<m<0,∴0<x<
 ;
;令f′(x)<0,∵x>0,-1<m<0,∴x>
 ;
;∴函数在(0,
 )上单调递增,在(
)上单调递增,在( ,+∞)上单调减;
,+∞)上单调减;当m≤-1时,f′(x)≤0,函数在(0,+∞)上单调递减.
分析:(1)求导函数,确定函数在区间
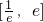 上的单调性,即可求最值;
上的单调性,即可求最值;(2)求导函数,对m分类讨论,利用导数的正负,可得函数f(x)的单调性.
点评:本题考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求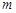 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).