题目内容
在直三棱柱ABC-A1B1C1中,∠BAC=
,AB=AC=AA1=1,D和E分别为棱AC、AB上的动点(不包括端点),若C1E⊥B1D,则线段DE长度的取值范围为( )
| π |
| 2 |
分析:由题设条件分别以AB,AC,AA1为x轴,y轴,z轴,作空间直角坐标系,则B1(1,0,1),C1(0,1,1),设E(t1,0,0),D(0,t2,0),t1,t2∈(0,1),则
=(t1,-1,-1),
=(-1,t2,-1),再由C1E⊥B1D,得t1+t2=1.由
=(t1,-t2,0),知|
| =
=
=
,由此能求出线段DE长度的取值范围.
| C1E |
| B1D |
| DE |
| DE |
| x12+x22 |
| x1 2+(1-x1)2 |
2(t1-
|
解答:解:∵直三棱柱ABC-A1B1C1中,
∠BAC=
,AB=AC=AA1=1,D和E分别为棱AC、AB上的动点(不包括端点),
∴分别以AB,AC,AA1为x轴,y轴,z轴,作空间直角坐标系,
则B1(1,0,1),C1(0,1,1),
设E(t1,0,0),D(0,t2,0),t1,t2∈(0,1),
则
=(t1,-1,-1),
=(-1,t2,-1),
∵C1E⊥B1D,
∴-t1-t2+1=0,
即t1+t2=1.
∵
=(t1,-t2,0),
∴|
| =
=
=
,
∵0<t1<1,
∴当t1=
时,|
|min=
=
,
当
|
| =
=1.
∴线段DE长度的取值范围为[
,1).
故选C.
∠BAC=
| π |
| 2 |
∴分别以AB,AC,AA1为x轴,y轴,z轴,作空间直角坐标系,
则B1(1,0,1),C1(0,1,1),
设E(t1,0,0),D(0,t2,0),t1,t2∈(0,1),
则
| C1E |
| B1D |
∵C1E⊥B1D,
∴-t1-t2+1=0,
即t1+t2=1.
∵
| DE |
∴|
| DE |
| t12+t22 |
=
| t12+(1-t1)2 |
=
2(t1-
|
∵0<t1<1,
∴当t1=
| 1 |
| 2 |
| DE |
|
| ||
| 2 |
当
| lim |
| t→1 |
| DE |
| lim |
| t→1 |
2(t1-
|
∴线段DE长度的取值范围为[
| ||
| 2 |
故选C.
点评:本题考查棱柱的结构特征,是基础题.解题时要认真审题,恰当地建立空间直角坐标系,利用空间向量求解.

练习册系列答案
相关题目
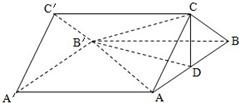 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,