Question

已知函数f(x)=(a＞0,x＞0).

(1)求证:f(x)在(0,+∞)上单调递增;

(2)若f(x)在［m,n］上的值域是［m,n］(0＜m＜n),求a的取值范围.

Answer 1

(1)证明:设0＜x₁＜x₂,则f(x₂)-f(x₁)=--(-)=.

∵x₂-x₁＞0,x₁＞0,x₂＞0,

∴f(x₂)-f(x₁)＞0.即f(x)在(0,+∞)上递增.

(2)解：由(1)知f(x)在［m,n］上递增,故

∴m、n是方程-=x的两根.

方程变形为ax²-x+a=0.                              (*)

问题转化为方程(*)有两不等正根,求a的取值范围.

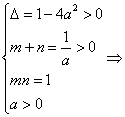0＜a＜,即a的取值范围为(0,).