Question

【题目】已知三棱锥A﹣BCD的所有棱长都相等，若AB与平面α所成角等于 ，则平面ACD与平面α所成角的正弦值的取值范围是（ ）
A.[ ， ]
B.[ ，1]
C.[ ﹣ ， + ]
D.[ ﹣ ，1]

Answer 1

【答案】A
【解析】解：∵三棱锥A﹣BCD的所有棱长都相等，

∴三棱锥A﹣BCD为正四面体，如图：

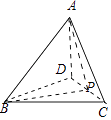
设正四面体的棱长为2，取CD中点P，连接AP，BP，

则∠BAP为AB与平面ADC所成角．

AP=BP= ，可得sin ，cos∠BAP= ．

设∠BAP=θ．

当CD与α平行且AB在面ACD外时，平面ACD与平面α所成角的正弦值最小，

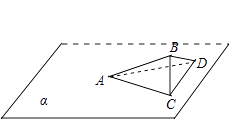
为sin（ ）=sin = ；

当CD与α平行且AB在面ACD内时，平面ACD与平面α所成角的正弦值最大，

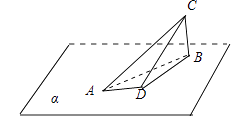
为sin（ ）=sin cos = ．

∴平面ACD与平面α所成角的正弦值的取值范围是[ ， ]．

故选：A．