题目内容
已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱.求：（1）圆柱的侧面积；
（2）x为何值时，圆柱的侧面积最大？
解:（1）圆锥及内接圆柱的轴截面如图所示.
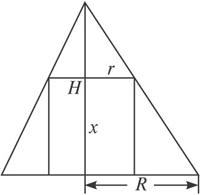
设所求的圆柱的底面半径为r，则S圆柱侧=2πrx.
∵
=
,∴r=R
x.
∴S圆柱侧=2πRx
x2(0＜x＜H).
（2）∵S圆柱侧=
x2+2πRx=
(x
)2+
,
故当x=
时,S圆柱侧最大，即当圆柱的高是已知圆锥的高的一半时，圆柱的侧面积最大.
练习册系列答案
名校课堂系列答案
相关题目
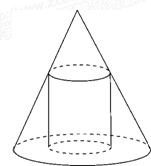已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱． 如图所示．
如图，已知一个圆锥的底面半径为R，高为h，在其中有一个高为x的内接圆柱（其中R，h均为常数）．
如图，已知一个圆锥的底面半径为R=1，高为h=2．，一个圆柱的下底面在圆锥的底面上，且圆柱的上底面为圆锥的截面，设圆柱的高为x．