题目内容
已知集合 .对于A=(a1,a2,…,an),B=(b1,b2,…,bn)∈Sn,定义
.对于A=(a1,a2,…,an),B=(b1,b2,…,bn)∈Sn,定义 ;λ(a1,a2,…,an)=(λa1,λa2,…,λan)(λ∈R);A与B之间的距离为
;λ(a1,a2,…,an)=(λa1,λa2,…,λan)(λ∈R);A与B之间的距离为 .
.(Ⅰ)当n=5时,设A=(1,2,1,2,5),B=(2,4,2,1,3),求d(A,B);
(Ⅱ)证明:若A,B,C∈Sn,且?λ>0,使
 ,则d(A,B)+d(B,C)=d(A,C);
,则d(A,B)+d(B,C)=d(A,C);(Ⅲ)记I=(1,1,…,1)∈S20.若A,B∈S20,且d(I,A)=d(I,B)=13,求d(A,B)的最大值.
【答案】分析:(Ⅰ) 当n=5时,直接利用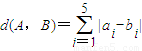 ,求得 d(A,B)的值.
,求得 d(A,B)的值.
(Ⅱ)设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn),则由题意可得?λ>0,使得
bi-ai=λ(ci-bi),其中i=1,2,…,n,由此计算 d(A,B)+d(B,C)的结果,计算d(A,C)的结果,从而得出结论
(Ⅲ) 根据x,y∈R,则有|x+y|≤|x|+|y|,可得所以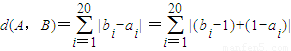
 ,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.
,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.
解答:(Ⅰ)解:当n=5时,由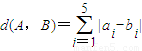 ,
,
得 d(A,B)=|1-2|+|2-4|+|1-2|+|2-1|+|5-3|=7,所以 d(A,B)=7.
(Ⅱ)证明:设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn).
因为?λ>0,使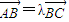 ,
,
所以?λ>0,使得 (b1-a1,b2-a2,…,bn-an)=λ((c1-b1,c2-b2,…,cn-bn),
所以?λ>0,使得 bi-ai=λ(ci-bi),其中i=1,2,…,n.
所以 bi-ai与ci-bi(i=1,2,…,n)同为非负数或同为负数.
所以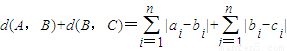
= =
=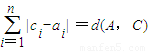 .
.
(Ⅲ) 首先证明如下引理:设x,y∈R,则有|x+y|≤|x|+|y|.
证明:因为-|x|≤x≤|x|,-|y|≤y≤|y|,所以-(|x|+|y|)≤x+y≤|x|+|y|,
即|x+y|≤|x|+|y|.
所以
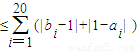
=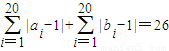 .
.
上式等号成立的条件为ai=1,或bi=1,所以 d(A,B)≤26.
对于 A=(1,1,…,1,14),B=(14,1,1,…,1),有 A,B∈S20,
且d(I,A)=d(I,B)=13,故d(A,B)=26.
综上,d(A,B)的最大值为26.
点评:本题主要考查新定义,两点间的距离公式,两个向量共线,绝对值不等式的性质应用,属于中档题.
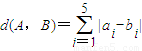 ,求得 d(A,B)的值.
,求得 d(A,B)的值.(Ⅱ)设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn),则由题意可得?λ>0,使得
bi-ai=λ(ci-bi),其中i=1,2,…,n,由此计算 d(A,B)+d(B,C)的结果,计算d(A,C)的结果,从而得出结论
(Ⅲ) 根据x,y∈R,则有|x+y|≤|x|+|y|,可得所以
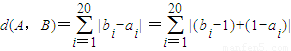
 ,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.
,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.解答:(Ⅰ)解:当n=5时,由
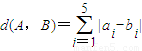 ,
,得 d(A,B)=|1-2|+|2-4|+|1-2|+|2-1|+|5-3|=7,所以 d(A,B)=7.
(Ⅱ)证明:设A=(a1,a2,…,an),B=(b1,b2,…,bn),C=(c1,c2,…,cn).
因为?λ>0,使
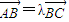 ,
,所以?λ>0,使得 (b1-a1,b2-a2,…,bn-an)=λ((c1-b1,c2-b2,…,cn-bn),
所以?λ>0,使得 bi-ai=λ(ci-bi),其中i=1,2,…,n.
所以 bi-ai与ci-bi(i=1,2,…,n)同为非负数或同为负数.
所以
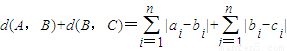
=
 =
=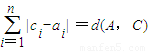 .
.(Ⅲ) 首先证明如下引理:设x,y∈R,则有|x+y|≤|x|+|y|.
证明:因为-|x|≤x≤|x|,-|y|≤y≤|y|,所以-(|x|+|y|)≤x+y≤|x|+|y|,
即|x+y|≤|x|+|y|.
所以

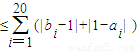
=
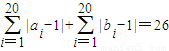 .
.上式等号成立的条件为ai=1,或bi=1,所以 d(A,B)≤26.
对于 A=(1,1,…,1,14),B=(14,1,1,…,1),有 A,B∈S20,
且d(I,A)=d(I,B)=13,故d(A,B)=26.
综上,d(A,B)的最大值为26.
点评:本题主要考查新定义,两点间的距离公式,两个向量共线,绝对值不等式的性质应用,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 属于τ;
属于τ; ,对于它的非空子集A,将A中的每个元素k,都乘以
,对于它的非空子集A,将A中的每个元素k,都乘以 再求和,(如A = {1,3,6},可求和得到
再求和,(如A = {1,3,6},可求和得到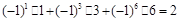 ),则对M的所有非空子集,这些和的总和是________________.
),则对M的所有非空子集,这些和的总和是________________.