题目内容
等比数列{an}的各项均为正数，且2a1+3a2=1，a32=9a2a6，
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log3a1+log3a2+…+log3an，求数列{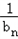
}的前n项和．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log3a1+log3a2+…+log3an，求数列{
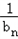}的前n项和．解：（Ⅰ）设数列{an}的公比为q，由a32=9a2a6得a32=9a42，所以q2=
．
由条件可知各项均为正数，故q=
．
由2a1+3a2=1得2a1+3a1q=1，所以a1=
．
故数列{an}的通项式为an=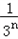
．
（Ⅱ）bn=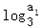
+
+…+
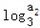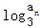=﹣（1+2+…+n）=﹣
，
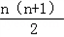故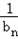
=﹣
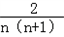=﹣2（
﹣
）
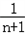则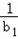
+
+…+
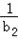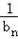=﹣2[（1﹣
）+（
﹣
）+…+（
﹣
）]=﹣
，
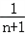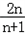所以数列{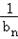
}的前n项和为﹣
．
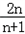．由条件可知各项均为正数，故q=
．由2a1+3a2=1得2a1+3a1q=1，所以a1=
．故数列{an}的通项式为an=
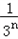．（Ⅱ）bn=
+
+…+
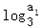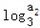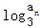=﹣（1+2+…+n）=﹣
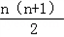，故
=﹣
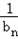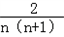=﹣2（
﹣
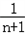）则
+
+…+
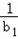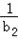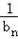=﹣2[（1﹣
）+（
﹣
）+…+（
﹣
）]=﹣
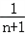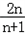，所以数列{
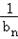}的前n项和为﹣
．
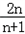练习册系列答案
相关题目
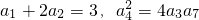，则数列{an}的通项公式为________．
，则数列{an}的通项公式为 ．