题目内容
(本小题满分14分)如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线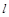 与圆
与圆 相交于
相交于 ,
, 两点,
两点,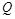 是
是 的中点,直线
的中点,直线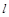 与
与 相交于点
相交于点 .
.

(1)求圆 的方程;
的方程;
(2)当 时,求直线
时,求直线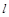 的方程.
的方程.
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
【答案】
(1) (2)
(2) 或
或 (3)是定值,为
(3)是定值,为 ,理由见解析
,理由见解析
【解析】
试题分析:(1)设圆 的半径为
的半径为 .
.
因为圆 与直线
与直线 相切,
相切,
 .
.
所以圆 的方程为
的方程为 .
……4分
.
……4分
(2)当直线 与
与 轴垂直时,易知
轴垂直时,易知 符合题意;
……5分
符合题意;
……5分
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 ,
,
 .
.
由 ,得
,得 .
.
 直线
直线 的方程为
的方程为 .
.
 所求直线
所求直线 的方程为
的方程为 或
或 .
……9分
.
……9分
(3)

 .
.
 =
= .
.
当直线 与
与 轴垂直时,得
轴垂直时,得 ,则
,则 又
又 ,
,
 .
.
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 .
.
由 解得
解得 .
.
 .
.
 .
.
综上所述, 是定值,且
是定值,且 .
……14分
.
……14分
考点:本小题主要考查直线与圆的位置关系、弦长公式的应用以及平面向量的运算,考查学生综合运用所学知识解决问题的能力和运算求解能力以及思维的严密性.
点评:本小题的易错点在于设直线方程时,忘记考虑斜率不存在的情况,所以做题时思路一定要严谨,步骤一定要规范.

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)