题目内容
已知函数f(x)=ax2+blnx在x=1处有极值| 1 | 2 |
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
分析:(1)函数f(x)=ax2+blnx在x=1处有极值
得到f(1)=
,f′(1)=0得到a、b即可;
(2)找到函数的定义域,在定义域中找到符合条件的驻点来讨论函数的增减性求出单调区间即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)找到函数的定义域,在定义域中找到符合条件的驻点来讨论函数的增减性求出单调区间即可.
解答:解:(1)因为函数f(x)=ax2+blnx,
所以f′(x)=2ax+
.
又函数f(x)在x=1处有极值
,
所以
即
可得a=
,b=-1.
(2)由(1)可知f(x)=
x2-lnx,其定义域是(0,+∞),
且f′(x)=x-
=
当x变化时,f′(x),f(x)的变化情况如下表:
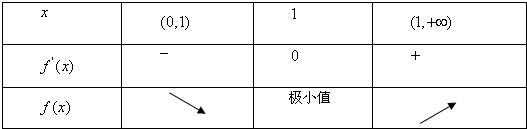
所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞)
所以f′(x)=2ax+
| b |
| x |
又函数f(x)在x=1处有极值
| 1 |
| 2 |
所以
|
|
可得a=
| 1 |
| 2 |
(2)由(1)可知f(x)=
| 1 |
| 2 |
且f′(x)=x-
| 1 |
| x |
| (x+1)(x-1) |
| x |
当x变化时,f′(x),f(x)的变化情况如下表:

所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞)
点评:考查学生利用导数研究函数极值的能力,利用导数研究函数增减性的能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目