Question

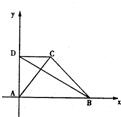如图，直角梯形ABCD中，AB∥CD，AB⊥AD，对角线AC⊥BD，且A（0，0），B（4，0）
（1）求点C的轨迹M；
（2）过点B的直线l交轨迹M于E，F两点，求证：AE⊥AF．

Answer 1

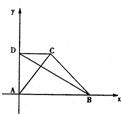解：如图建立坐标系，设C（x，y）（x≠0），
则D（0，y），=（x，y），=（-4，y）∵⊥，?y²=4x（x≠0）
∴所求的轨迹M是除去顶点的抛物线
（2）当直线l垂足x轴时，命题显然处理，当斜率不存在时，设直线l：y=k（x-4）（k≠0）
联立y²=4x?k²x₂-（8k²+4）x+16k²=0，；设E（x₁，y₁），F（x₂，y₂）
则x₁+x₂=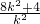；x₁x₂=16而y₁y₂=k²（x₁-4）（x₂-4）=-16
∴x₁x₂+y₁y₂=0，则AE⊥AF
分析：（1）直接设C（x，y）（x≠0），则D（0，y），由AC⊥BD，由斜率之际为-1，或向量的数量积为0，
直接可求得点C的轨迹方程，再由方程确定轨迹即可．
（2）设E（x₁，y₁），F（x₂，y₂），AE⊥AF?x₁x₂+y₁y₂=0．故只需联力方程、消元、维达定理纠结即可．
点评：本题考查直接法求轨迹方程、直线和抛物线的位置关系问题、考查运算能力和转化思想．