题目内容
若函数y=f(x)的定义域为[-1,4],则函数y=f(2x-1)的定义域为
- A.
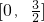
- B.
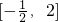
- C.
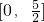
- D.

C
分析:由函数y=f(x)的定义域为[-1,4],对于函数y=f(2x-1),-1≤2x-1≤4,解得x的范围即为所求.
解答:∵函数y=f(x)的定义域为[-1,4],则对函数y=f(2x-1),应有
-1≤2x-1≤4,解得 0≤x≤ ,
,
故选C.
点评:本题考查抽象函数的定义域的求法,体现了换元的数学思想,列出不等式-1≤2x-1≤4 是解题的关键.
分析:由函数y=f(x)的定义域为[-1,4],对于函数y=f(2x-1),-1≤2x-1≤4,解得x的范围即为所求.
解答:∵函数y=f(x)的定义域为[-1,4],则对函数y=f(2x-1),应有
-1≤2x-1≤4,解得 0≤x≤
 ,
,故选C.
点评:本题考查抽象函数的定义域的求法,体现了换元的数学思想,列出不等式-1≤2x-1≤4 是解题的关键.

练习册系列答案
相关题目