题目内容
(本题满分12分)已知数列 的首项
的首项 ,
,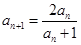 ,
,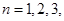 ….
….
(Ⅰ)证明:数列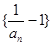 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前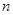 项和
项和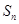 .
.
(Ⅰ)见解析(Ⅱ)
解析试题分析:(Ⅰ)
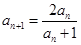 ,
,
 ,
, 
 ,又
,又 ,
,
 ,
,  数列
数列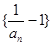 是以为
是以为 首项,
首项, 为公比的等比数列. …………4分
为公比的等比数列. …………4分
(Ⅱ)由(Ⅰ)知 ,即
,即 , ……………6分
, ……………6分
 . 设
. 设 …
… , ① ……8分
, ① ……8分
则 …
… ,② ……………………9分
,② ……………………9分
由① ②得
②得 …
… ,…………10分
,…………10分
 .又
.又 …
… . …………11分
. …………11分
 …………12分
…………12分
考点:等比数列证明及求前n项和
点评:一般数列构造成等差等比新数列求解

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
设 ,且
,且 ,则 ( )
,则 ( )
A. | B. | C. | D. |
 共有
共有 项(整数
项(整数 ),首项
),首项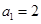 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数 ⑴求
⑴求 ,数列
,数列 满足
满足
 ;
; ,求
,求 的最大值.
的最大值.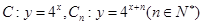 ,从
,从 上的点
上的点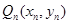 作
作 轴的垂线,交
轴的垂线,交 于点
于点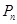 ,再从点
,再从点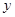 轴的垂线,交
轴的垂线,交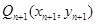 ,
,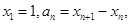
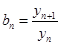 .。
.。 求数列
求数列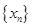 的通项公式;
的通项公式;  记
记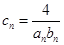 ,数列
,数列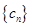 的前
的前 项和为
项和为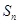 ,试比较
,试比较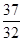 的大小
的大小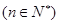 ;
;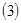 记
记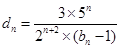 ,数列
,数列 的前
的前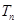 ,试证明:
,试证明: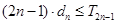 。
。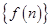 的前n项和为
的前n项和为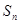 ,且
,且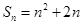 .
.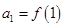 ,
,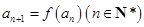 ,求证数列
,求证数列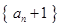 是等比数列,并求数
是等比数列,并求数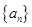 的前
的前 项和
项和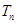 .
.  满足
满足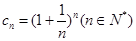 ,试证明:
,试证明: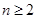 时,有
时,有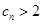 ;
;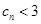 .
.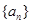 和
和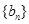 满足:
满足: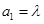 ,
,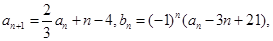 其中
其中 为实数,
为实数,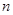 为正整数.
为正整数.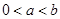 ,
,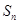 为数列
为数列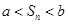 ?若存在,求
?若存在,求 满足
满足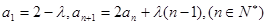
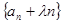 为等比数列;
为等比数列; 以及前n项和
以及前n项和 ;
; 都有
都有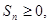 求
求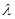 的取值范围。
的取值范围。