题目内容

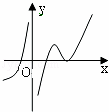
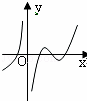
设函数f（x）在定义域内可导，y=f（x）的图象如图所示，则导函数y=f′（x）可能（　　）

　

A．

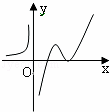
B．

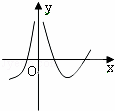
C．

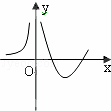
D．

考点：

函数的单调性与导数的关系．

专题：

数形结合法．

分析：

先根据函数f（x）的图象判断单调性，从而得到导函数的正负情况，最后可得答案．

解答：

解：原函数的单调性是：当x＜0时，增；当x＞0时，单调性变化依次为增、减、增

故当x＜0时，f′（x）＞0；当x＞0时，f′（x）的符号变化依次为+、﹣、+．

故选D．

点评：

本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．

练习册系列答案
相关题目
设函数f（x）是定义在[-1，0）∪（0，1]上的奇函数，当x∈[-1，0）时，f(x)=
a
x
-x2（a为实数）．
（1）若f(
1
2
)=-2，求a的值；
（2）当x∈（0，1]时，求f（x）的解析式；
（3）当a＞2时，试判断f（x）在（0，1]上的单调性，并证明你的结论．
设函数=f（x）在（-∞，+∞）内有定义，对于给定的正数K，定义函数fK（x）=
f(x)，f(x)≤K
K，f(x)＞K.
取函数f（x）=2-|x|．当K=
1
2
时，函数fK（x）的单调递增区间为（　　）
A、（-∞，0）
B、（0，+∞）
C、（-∞，-1）
D、（1，+∞）
设函数f（x）在（-∞，+∞）内有定义，对于给定的正数K，定义函数：fK（x）=
f(x)，f(x)≤K
1
f(x)
，f(x)＞K
，取函数f（x）=a11（a＞1）．当K=
1
a
时，函数f（x）值域是（　　）
A、[0，
1
a
]∪[1，a）
B、（0，
1
a
]∪[1，a]
C、（0，1]∪[
1
a
，a）
D、（0，
1
a
]∪[1，a）
（2012•浙江）设函数f（x）是定义在R上的周期为2的偶函数，当x∈[0，1]时，f（x）=x+1，则f(
3
2
)=
3
2
3
2
．
设函数f（x）是定义在（-∞，+∞）上的增函数，是否存在这样的实数a，使得不等式f（1-ax-x2）＜f（2-a）对于任意x∈[0，1]都成立？若存在，试求出实数a的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网