题目内容
已知O是△ABC的外心，AB=6，AC=10，若
=x•
+y•
且2x+10y=5，则cos∠BAC= ．
| AO |
| AB |
| AC |
分析：当△ABC是锐角三角形时，取AB、AC的中点D、E，连结OD、OE．由三角形外接圆的性质得OD⊥AB且OE⊥AC，由此利用直角三角形中三角函数的定义和数量积的公式，算出
•
=
|
|2=18且
•
=
|
|2=50．然后在等式
=x
+y
的两边分别与
、
作数量积，将得到的等式与2x+10y=5组成方程组联解，算出
•
=20，可得cos∠BAC的值．最后由△ABC是以AC为斜边的直角三角形时，算出cos∠BAC=
，即可得出满足条件的cos∠BAC值．
| AO |
| AB |
| 1 |
| 2 |
| AB |
| AO |
| AC |
| 1 |
| 2 |
| AC |
| AO |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| 3 |
| 5 |
解答：解：分别取AB、AC的中点D、E，连结OD、OE，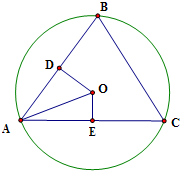
（i）当x≠0时，
∵O是锐角△ABC的外接圆的圆心，D、E分别为AB、AC的中点，
∴OD⊥AB，OE⊥AC．
由此可得Rt△AOD中，cos∠OAD=
=
•
，
∴
•
=|
|•|
|cos∠OAD=|
|•|
|•
•
=
|
|2=18．
同理可得
•
=
|
|2=50．
∵
=x•
+y•
，
∴等式的两边都与
作数量积，得
•
=x
2+y
•
，化简得18=36x+y
•
，…①
同理，等式的两边都与
作数量积，化简得50=x
•
+100y，…②
又∵根据题意知2x+10y=5，…③
∴①②③联解，可得
•
=20，由此可得
=
=
（ii）当x=0时，
=y•
且10y=5，可得
=
∴△ABC是以AC为斜边的直角三角形，可得cos∠BAC=
=
．
故答案为：
或
（i）当x≠0时，
∵O是锐角△ABC的外接圆的圆心，D、E分别为AB、AC的中点，
∴OD⊥AB，OE⊥AC．
由此可得Rt△AOD中，cos∠OAD=
| ||
|
| 1 |
| 2 |
| ||
|
∴
| AO |
| AB |
| AO |
| AB |
| AO |
| AB |
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
| AB |
同理可得
| AO |
| AC |
| 1 |
| 2 |
| AC |
∵
| AO |
| AB |
| AC |
∴等式的两边都与
| AB |
| AO |
| AB |
| AB |
| AB |
| AC |
| AB |
| AC |
同理，等式的两边都与
| AC |
| AB |
| AC |
又∵根据题意知2x+10y=5，…③
∴①②③联解，可得
| AB |
| AC |
| ||||
|
| 20 |
| 6×10 |
| 1 |
| 3 |
（ii）当x=0时，
| AO |
| AC |
| AO |
| 1 |
| 2 |
| AC |
∴△ABC是以AC为斜边的直角三角形，可得cos∠BAC=
| AB |
| AC |
| 3 |
| 5 |
故答案为：
| 1 |
| 3 |
| 3 |
| 5 |
点评：本题着重考查了三角形外接圆的性质、锐角的三角函数在直角三角形中的定义、向量量的数量积公式和方程组的解法等知识，属于中档题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目