题目内容
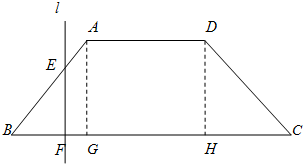 如图,已知底角为60°的等腰梯形ABCD,底边BC长为7cm,腰长为4cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出直线l左边部分的面积y与x的函数关系式.
如图,已知底角为60°的等腰梯形ABCD,底边BC长为7cm,腰长为4cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出直线l左边部分的面积y与x的函数关系式.
分析:过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.然后分别讨论F点在BG,GH,HC上时,直线L左边部分的形状,并分别代入相应的面积公式,即可得到直线l左边部分的面积y与x的函数关系式.
解答:解:过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
因为ABCD是等腰梯形,底角为60°,AB=4cm,所以BG=HC=2cm,AG=DH=2
cm
又BC=7cm,所以AD=GH=3cm.
(1)当点F在BG上时,即x∈(0,2]时,y=
x2;
(2)当点F在GH上时,
即x∈(2,5]时,y=2
+(x-2)•2
=2
x-2
;
(3)当点F在HC上时,即x∈(5,7]时,y=S五边形ABFED=S梯形ABCD-SRt△CEF=10
-
(7-x)2.
所以,函数解析式为y=
因为ABCD是等腰梯形,底角为60°,AB=4cm,所以BG=HC=2cm,AG=DH=2
| 3 |
又BC=7cm,所以AD=GH=3cm.
(1)当点F在BG上时,即x∈(0,2]时,y=
| ||
| 2 |
(2)当点F在GH上时,
即x∈(2,5]时,y=2
| 3 |
| 3 |
| 3 |
| 3 |
(3)当点F在HC上时,即x∈(5,7]时,y=S五边形ABFED=S梯形ABCD-SRt△CEF=10
| 3 |
| 1 |
| 2 |
| 3 |
所以,函数解析式为y=
|
点评:本题考查的知识点是分段函数的应用,求分段函数的解析式,要分如下几个步骤:①分析图象被分成的段数,以确定函数所分的段数;②分类讨论,写出各段的解析式③写出分段函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

