题目内容
四棱锥P—ABCD中,侧面APD⊥底面ABCD,∠APD=∠BAD=90°,∠ADC=60°,E为AD上一点,AE=2,AP=6,AD=CD=8,AB=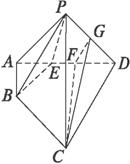
(1)求证:AB⊥PE;
(2)求证:CD∥平面PBE;
(3)求二面角A-PD-C的大小.
(1)证明:∵∠BAD=90°,即AB⊥AD,

又侧面APD⊥底面ABCD,∴AB⊥面APD.
∵PE![]() 面APD,∴AB⊥PE.
面APD,∴AB⊥PE.
(2)证明:∵∠BAD=90°,AB=23,AE=2,
∴∠AEB=60°.
∵∠ADC=60°,CD,BE共面,∴CD∥BE.
又CD![]() 面PBE,BE
面PBE,BE![]() 面PBE,∴CD∥面PBE.
面PBE,∴CD∥面PBE.
(3)解:在面ABCD内作CF⊥AD,垂足为F,
∵侧面APD⊥底面ABCD,∴CF⊥面APD.
在面APD内作FG⊥PD,垂足为G,连结CG,则CG⊥PD.
∴∠CGF是二面角APDC的平面角.
∴FC=8sin60°=![]() ,FD=8cos60°=4.
,FD=8cos60°=4.
∵AP⊥PD,∴AP=2FG=6,于是FG=3.
∴tan∠CGF=![]() .
.
∴∠CGF=arctan![]() 为所求.
为所求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
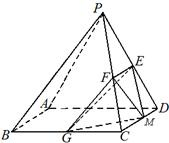 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.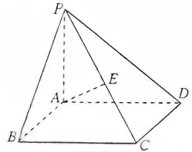 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2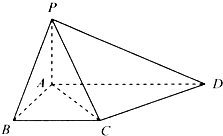 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.