题目内容
四面体ABCD中，已知AB=3cm，S△ABC=15cm2，S△ABC=12cm2，面ABC与ABD所成的二面角为30°，则四面体的体积为（ ）
分析：设AD=BD，CA=CB，取AB中点O，连接DO，CO，则∠DOC=30°，由AB=3cm，S△ABD=15cm2，S△ABC=12cm2，知DO=10，CO=8，由此能求出四面体ABCD的体积．
解答：
解：设AD=BD，CA=CB，取AB中点O，连接DO，CO，
则∠DOC为面ABC与ABD所成的二面角的平面角，
∴∠DOC=30°，
∵AB=3cm，S△ABD=15cm2，S△ABC=12cm2，
∴DO=10，CO=8，
作DE⊥OC，交OC于E，
∵DO⊥AB，CO⊥AB，
∴AB⊥平面DOC，
∴DE⊥AB，∴DE⊥平面ABC，
∴DE=
DO=5，
∴四面体ABCD的体积V=
×S△ABC×DE=
×12×5=20cm3．
解：设AD=BD，CA=CB，取AB中点O，连接DO，CO，则∠DOC为面ABC与ABD所成的二面角的平面角，
∴∠DOC=30°，
∵AB=3cm，S△ABD=15cm2，S△ABC=12cm2，
∴DO=10，CO=8，
作DE⊥OC，交OC于E，
∵DO⊥AB，CO⊥AB，
∴AB⊥平面DOC，
∴DE⊥AB，∴DE⊥平面ABC，
∴DE=
| 1 |
| 2 |
∴四面体ABCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
点评：本题考查四面积的体积的求法，综合性强，难度大，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
在四面体ABCD中，已知DA=DB=DC=1，且DA、DB、DC两两互相垂直，在该四面体表面上与点A距离为2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
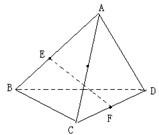如图，在四面体ABCD中，已知所有棱长都为a，点E、F分别是AB、CD的中点．