题目内容
某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为:p=
(0≤x≤8),若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(I)求f(x)的表达式;
(II)宿舍应建在离工厂多远处,可使总费用f(x)最小,并求最小值.
| k | 3x+5 |
(I)求f(x)的表达式;
(II)宿舍应建在离工厂多远处,可使总费用f(x)最小,并求最小值.
分析:(Ⅰ)根据距离为1km时,测算宿舍建造费用为100万元,可求k的值,由此,可得f(x)的表达式;
(Ⅱ)f(x)=
+2(3x+5)-5,利用基本不等式,即可求出函数的最小值.
(Ⅱ)f(x)=
| 800 |
| 3x+5 |
解答:解:(Ⅰ)根据题意,距离为1km时,测算宿舍建造费用为100万元
∴100=
,∴k=800(3分)
∴f(x)=
+5+6x,0≤x≤8 (7分)
(Ⅱ)∵f(x)=
+2(3x+5)-5≥80-5 (11分)
当且仅当
=2(3x+5)即x=5时f(x)min=75. (14分)
答:宿舍应建在离厂5km处可使总费用f(x)最小为75万元. (15分)
∴100=
| k |
| 3×1+5 |
∴f(x)=
| 800 |
| 3x+5 |
(Ⅱ)∵f(x)=
| 800 |
| 3x+5 |
当且仅当
| 800 |
| 3x+5 |
答:宿舍应建在离厂5km处可使总费用f(x)最小为75万元. (15分)
点评:本题考查函数模型的构建,考查利用基本不等式求函数的最值,注意基本不等式的使用条件.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
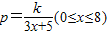 ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.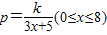 ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.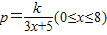 ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.