题目内容
已知平行六面体ABCD—A′B′C′D′中，AB=3，AD=4，AA′=5,∠BAA′=∠DAA′=
∠BAD=60°，求AC′的长.
思路分析：结合图形容易将向量
用
、
、
表示出来，再进行平方转化成模与数量积的关系易解.
解：∵|
|2=
=(
)2
=(
)2
=
=9+16+25+2(3×4+3×5+4×5)=97，
∴|
|=
，即AC′的长为
.
方法归纳 公式：（a+b+c）·（a+b+c）=(a+b+c)2=|a|2+|b|2+|c|2+2a·b+2b·c+2c·a应该牢记，并且能够熟练应用.
练习册系列答案
相关题目
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
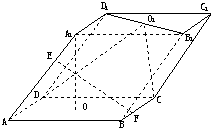如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
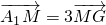，设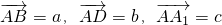
，用向量a、b、c表示向量
；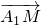