题目内容
已知函数f(x)=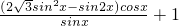 .
.
(Ⅰ)求f(x)的定义域及最小正周期;
(Ⅱ)求f(x)在区间[ ,
, ]上的最值.
]上的最值.
解:(Ⅰ)由sinx≠0 得,x≠kπ (k∈z),
故f(x)的定义域为{x|x≠kπ,k∈zZ}.…(2分)
因为f(x)=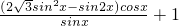 =(2
=(2 sinx-2cosx)cosx+1=
sinx-2cosx)cosx+1= sin2x-cos2x=2sin(2x-
sin2x-cos2x=2sin(2x- ),…(6分)
),…(6分)
所以f(x)的最小正周期 T= =π.…(7分)
=π.…(7分)
(II)由 x∈[ ,
, ],可得 2x∈[
],可得 2x∈[ ,π],故2x-
,π],故2x- ∈[
∈[ ,
, ],…..(9分)
],…..(9分)
故当2x- =
= ,即x=
,即x= 时f(x)取得最小值为-1,….(11分)
时f(x)取得最小值为-1,….(11分)
当2x- =
= ,即x=
,即x= 时,函数f(x)取得最大值为 2.….(13分)
时,函数f(x)取得最大值为 2.….(13分)
分析:(Ⅰ)由函数的解析式求得sinx≠0,由此求得函数的定义域.利用三角函数的恒等变换化简函数f(x)的解析式为 2sin(2x- ),由此求得它的最小正周期.
),由此求得它的最小正周期.
(II)由 x∈[ ,
, ],根据正弦函数的定义域和值域,求得函数f(x)的最值.
],根据正弦函数的定义域和值域,求得函数f(x)的最值.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的定义域和值域,属于中档题.
故f(x)的定义域为{x|x≠kπ,k∈zZ}.…(2分)
因为f(x)=
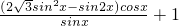 =(2
=(2 sinx-2cosx)cosx+1=
sinx-2cosx)cosx+1= sin2x-cos2x=2sin(2x-
sin2x-cos2x=2sin(2x- ),…(6分)
),…(6分)所以f(x)的最小正周期 T=
 =π.…(7分)
=π.…(7分)(II)由 x∈[
 ,
, ],可得 2x∈[
],可得 2x∈[ ,π],故2x-
,π],故2x- ∈[
∈[ ,
, ],…..(9分)
],…..(9分)故当2x-
 =
= ,即x=
,即x= 时f(x)取得最小值为-1,….(11分)
时f(x)取得最小值为-1,….(11分)当2x-
 =
= ,即x=
,即x= 时,函数f(x)取得最大值为 2.….(13分)
时,函数f(x)取得最大值为 2.….(13分)分析:(Ⅰ)由函数的解析式求得sinx≠0,由此求得函数的定义域.利用三角函数的恒等变换化简函数f(x)的解析式为 2sin(2x-
 ),由此求得它的最小正周期.
),由此求得它的最小正周期.(II)由 x∈[
 ,
, ],根据正弦函数的定义域和值域,求得函数f(x)的最值.
],根据正弦函数的定义域和值域,求得函数f(x)的最值.点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|