Question

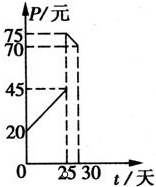
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：

第t天	5	15	20	30
Q/件	35	25	20	10

（1）根据题设条件，写出该商品每件的销售价格P与时间t的函数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）．

Answer 1

分析：（1）根据图象可知，每件商品的销售价格P与时间t的函数关系式满足一次函数，根据图象中所提供的点进行求解
（2）由日销售金额=每件的销售价格×日销售量可得，且由确表格中所提供的数据可知Q=t-40，从而结合（1）可得y=

-t2+20t+800 0＜t＜25 t2-140t+4000 ，25≤t≤30

，利用二次函数的性质进行求解最大值

解答：解：（1）根据图象，每件商品的销售价格P与时间t的函数关系式为：P=

t+20，0＜t＜25 -t+100，25≤t≤30.

(t∈N*)
Q=40-t
（2）设日销售金额为y元，则y=

-t2+20t+800 0＜t＜25 t2-140t+4000 ，25≤t≤30

=

-(t-10)2+900，0＜t＜25 (t-70)2-900，25≤t≤30

若0＜t＜25（t∈N^*），则当t=10时，y_max=900
若25≤t≤30，（t∈N^*），则当t=25时，y_max=1125
由1125＞900，知y_max=1125
这种商品日销售额的最大值为1125元，30天中的第25天的日销售额最大．

点评：本题主要考查了利用数学知识解决实际问题的能力，解题的关键是要把实际问题转化为数学问题，利用数学中二次函数的知识进行求解函数的最值