Question

设点P（x₀，y₀）在直线x=m（y≠±m，0＜m＜1）上，过点P作双曲线x²-y²=1的两条切线PA、PB，切点为A、B，定点M(

1

m

，0)．
（1）求证：三点A、M、B共线．
（2）过点A作直线x-y=0的垂线，垂足为N，试求△AMN的重心G所在曲线方程．

Answer 1

分析：（1）先根据题意设A（x₁，y₁），B（x₂，y₂），将切线PA的方程代入双曲线的方程，消去y得到关于x的一元二次方程，再结合根的判别式等于0即可表示出切线的斜率，因此PA的方程和PB的方程都可以利用A，B两点的坐标表示，又P在PA、PB上，得到点A（x₁，y₁），B（x₂，y₂）都在直线y₀y=mx-1上，从而证得三点A、M、B共线，从而解决问题．
（2）设重心G（x，y），欲求△AMN的重心G所在曲线方程，即求出其坐标x，y的关系式，利用点A在双曲线上即可得重心G所在曲线方程．

解答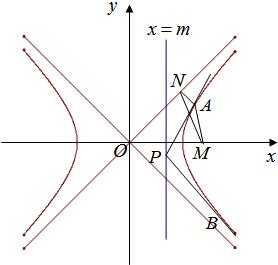：证明：（1）设A（x₁，y₁），B（x₂，y₂），
由已知得到y₁y₂≠0，且x₁²-y₁²=1，x₂²-y₂²=1，
设切线PA的方程为：y-y₁=k（x-x₁）由

y-y1=k(x-x1) x2-y2=1

得（1-k²）x²-2k（y₁-kx₁）x-（y₁-kx₁）²-1=0
从而△=4k²（y₁-kx₁）²+4（1-k²）（y₁-kx₁）²+4（1-k²）=0，
解得k=

x1

y1

因此PA的方程为：y₁y=x₁x-1
同理PB的方程为：y₂y=x₂x-1
又P（m，y₀）在PA、PB上，所以y₁y₀=mx₁-1，y₂y₀=mx₂-1
即点A（x₁，y₁），B（x₂，y₂）都在直线y₀y=mx-1上
又M(

1

m

，0)也在直线y₀y=mx-1上，所以三点A、M、B共线

（2）垂线AN的方程为：y-y₁=-x+x₁，
由

y-y1=-x+x1 x-y=0

得垂足N(

x1+y1

2

，

x1+y1

2

)，
设重心G（x，y）
所以

x= 1 3 (x1+ 1 m + x1+y1 2 ) y= 1 3 (y1+0+ x1+y1 2 )

解得

x1= 9x-3y- 3 m 4 y1= 9y-3x+ 1 m 4

由x₁²-y₁²=1可得(3x-3y-

1

m

)(3x+3y-

1

m

)=2即(x-

1

3m

)2-y2=

2

9

为重心G所在曲线方程

点评：本小题主要考查直线与圆锥曲线的综合问题、三角形重心、双曲线的标准方程的问题等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．