题目内容
已知 .求证:
.求证: .
.
证明:左减右得: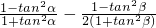
=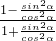 -
-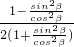
=cos2α-sin2α-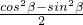
=1-2sin2α-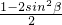 .①
.①
∵sinθ+cosθ=2sinα ②
sinθ•cosθ=sin2β ③
∴②2=1+2×③得:4sin2α=1+2sin2β,代入①得:①式等0.
即左边等于右边.
故结论得证.
分析:先左减右并把正切用正弦以及余弦表示出来,整理得到1-2sin2α-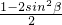 ;再结合sinθ+cosθ=2sinα以及sinθ•cosθ=sin2β 消去θ即可得到结论.
;再结合sinθ+cosθ=2sinα以及sinθ•cosθ=sin2β 消去θ即可得到结论.
点评:本题主要考查三角函数恒等式的证明.解决这类问题的关键在于对公式的熟练掌握以及灵活运用.
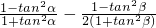
=
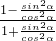 -
-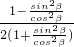
=cos2α-sin2α-
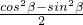
=1-2sin2α-
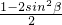 .①
.①∵sinθ+cosθ=2sinα ②
sinθ•cosθ=sin2β ③
∴②2=1+2×③得:4sin2α=1+2sin2β,代入①得:①式等0.
即左边等于右边.
故结论得证.
分析:先左减右并把正切用正弦以及余弦表示出来,整理得到1-2sin2α-
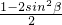 ;再结合sinθ+cosθ=2sinα以及sinθ•cosθ=sin2β 消去θ即可得到结论.
;再结合sinθ+cosθ=2sinα以及sinθ•cosθ=sin2β 消去θ即可得到结论.点评:本题主要考查三角函数恒等式的证明.解决这类问题的关键在于对公式的熟练掌握以及灵活运用.

练习册系列答案
相关题目
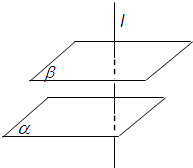 求证:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面.(要求:根据图形,写出已知、求证,并给出证明过程)
求证:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面.(要求:根据图形,写出已知、求证,并给出证明过程)