题目内容
如图：正方形的边长为1，E、F分别为BC、CD边上的动点，且∠EAF＝45°，问E在何处时，四边形AECF的面积最大，最大面积是多少？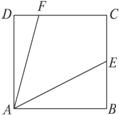
解：设∠EAB=θ，则S四边形AECF=S正方形ABCD-S△ABE-S△ADF
=1-［
tanθ+
tan（
-θ）］
=1-
［tanθ+
］
=1-
·
=
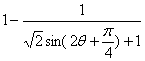.∵0≤θ≤
，∴2θ+
∈［
，
］
∴sin(2θ+π4)∈［
，1］.
∴S四边形AECF≤2-2，当θ=π8时，S四边形AECF取到最大值2-
.
答：当E点距B点（2-1）处（E在BC上且使得∠BAE=π8）时，SAECF取到最大值2-2.
练习册系列答案
相关题目
的边长为１，
，
分别为边
，
上的点．当
的周长为２时，求
的大小．
的边长为
，平面
到正方形各顶点的距离都是
，
分别是
，
上的点，且
．
平面
；
的长．
的边长为１，
，
分别为边
，
上的点．当
的周长为２时，求
的大小．
的边长为
，延长
至
，使
，连接
，则
B．
C．
D．
的边长为
，延长
至
，使
，连接 
、
， 则
