题目内容
(本小题满分12分)
已知函数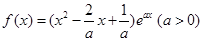
(I)当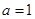 时,求函数
时,求函数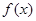 的图象在点A(0,
的图象在点A(0,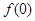 )处的切线方程;
)处的切线方程;
(II)讨论函数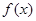 的单调性;
的单调性;
(Ⅲ)是否存在实数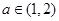 ,使
,使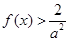 当
当 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数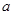 ;若不存在,请说明理由.
;若不存在,请说明理由.
解(I) .
.
(II) 在
在 ,
, 为增函数,
为增函数, 在
在 为减函数。
为减函数。
(Ⅲ)符合条件的实数 不存在.
不存在.
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)运用了导数的几何意义求解曲线的切线方程问题。
(2)利用导数的运算,和导数与不等式的关系,求解得到函数的单调区间。
(3)对于不等式的恒成立问题可以转化为求解新函数的最值问题,来得到参数的取值范围的求解的这样的数学思想的运用。
解(I) 时,
时, ,
,

于是 ,
, ,
,
所以函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为
即 .
………………………… ……………… 2分
.
………………………… ……………… 2分
(II)
= ,
,
∵ ,∴ 只需讨论
,∴ 只需讨论 的符号. ……………… 4分
的符号. ……………… 4分
ⅰ)当 >2时,
>2时, >0,这时
>0,这时 >0,所以函数
>0,所以函数 在(-∞,+∞)上为增函数.
在(-∞,+∞)上为增函数.
ⅱ)当 = 2时,
= 2时, ≥0,函数
≥0,函数 在(-∞,+∞)上为增函数.
在(-∞,+∞)上为增函数.
……………… 6分
ⅲ)当0< <2时,令
<2时,令 =
0,解得
=
0,解得 ,
, .
.
当 变化时,
变化时, 和
和 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
∴ 在
在 ,
, 为增函数,
为增函数, 在
在 为
为
减函数……………… 8分
(Ⅲ)当 ∈(1,2)时,
∈(1,2)时, ∈(0,1).由(2)知
∈(0,1).由(2)知 在
在 上是减函数,在
上是减函数,在 上是增函数,故当
上是增函数,故当 ∈(0,1)时,
∈(0,1)时, ,所以
,所以 当
当 ∈(0,1)时恒成立,等价于
∈(0,1)时恒成立,等价于 恒成立.……10分
恒成立.……10分
当 ∈(1,2)时,
∈(1,2)时, ,设
,设 ,则
,则 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得 ,即
,即 ∈(1,2)时
∈(1,2)时 恒成立,因此,符合条件的实数
恒成立,因此,符合条件的实数 不存在. ……………… 12分
不存在. ……………… 12分

