题目内容
(本小题满分12分)
某校高三年级要从 名男生
名男生 和
和 名女生
名女生 中任选
中任选 名代表参加学校的演讲比赛。
名代表参加学校的演讲比赛。
(I)求男生 被选中的概率
被选中的概率
(II)求男生 和女生
和女生 至少一人被选中的概率。
至少一人被选中的概率。
(I) (II)
(II)
解析试题分析:(I)所有的选择方法有 共
共 种,而男生
种,而男生 被选中的情况有
被选中的情况有 ,共
,共 种,
种,
所以男生 被选中的概率为
被选中的概率为 ; ……6分
; ……6分
(II)男生 和女生
和女生 至少一人被选中的情况有
至少一人被选中的情况有 共
共 种,所以男生
种,所以男生 和女生
和女生 至少一人被选中的概率为
至少一人被选中的概率为 . ……12分
. ……12分
考点:本小题考查了古典概型的应用以及应用概率知识解决实际问题的能力.
点评:古典概型是基本事件个数有限,每个基本事件发生的概率相等的一种概率模型,其概率等于随机事件所包含的基本事件的个数与基本事件总个数的比值.

练习册系列答案
相关题目
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投 次:在
次:在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在 处的命中率
处的命中率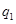 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 | 0 | 2 | 3 | 4 | 5 |
 |  |  |  | 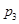 |  |
 的值;
的值; (2) 求随机变量
(2) 求随机变量 的数学期望
的数学期望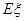 ;
;(3) 试比较该同学选择都在
 处投篮得分超过
处投篮得分超过 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过 分的概率的大小.
分的概率的大小.  中,平面区域
中,平面区域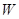 中的点的坐标
中的点的坐标 满足
满足 ,从区域
,从区域 .
. ,
, ,求点
,求点 位于第四象限的概率;
位于第四象限的概率; 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为 ,求
,求 的概率.
的概率.  ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数 的分布列及数学期望.
的分布列及数学期望. 小时,种植一捆沙棘用时
小时,种植一捆沙棘用时 小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
小时,应如何分配A,B两组的人数,使植树活动持续的时间最短? 小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.  ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示 的面试,第4组中有
的面试,第4组中有 名学生被考官
名学生被考官
 名学生被考官D面试,求
名学生被考官D面试,求