题目内容
| ∫ | 2 0 |
分析:将(0,2)区间分为(0,1)和(1,2),分别化简2-|1-x|,转化成
(2-|1-x|)dx=∫01(1+x)dx+∫12(3-x)dx,求解即可.
| ∫ | 2 0 |
解答:解:
(2-|1-x|)dx=∫01(1+x)dx+∫12(3-x)dx
=(x+
x2)|01+(3x-
x2)|12
=(1+
-0)+(6-2-3+
)
=3
故答案为:3
| ∫ | 2 0 |
=(x+
| 1 |
| 2 |
| 1 |
| 2 |
=(1+
| 1 |
| 2 |
| 1 |
| 2 |
=3
故答案为:3
点评:本题主要考查了定积分、定积分的应用、导数等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元). 件,则月平均利润
件,则月平均利润 (元),
(元),
 得
得
 时
时 ;
;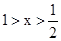 时
时
 得
得 取得最大值.
取得最大值.